一、众数

统计数据经过整理和显示后，我们对数据分布的类型和特点就有了一个大致的了解，但这种了解只是表面上的，还缺少代表性的数量特征值准确地描述出统计数据的分布。为进一步掌握数据分布的特征和规律，进行更深入的分析，还需要找到反应数据分布特征的各个代表值。对统计数据分布的特征，可以从三个方面进行测度和描述：一是分布的集中趋势，反映各个数据向其中心值靠拢或聚集的程度；二是分布的离散程度，反应各个数据远离其中心值的趋势；三是分布的偏态和峰度反映数据分布的形状。这三个方面分别反映了数据分布特征的不同侧面，本章将重点讨论这些代表值的计算方法、特点及其应用场合。

集中趋势是指一组数据向某一中心值靠拢的倾向，测度集中趋势也就是寻找数据一般水平的代表值或中心值。反映数据集中趋势的测度值主要包括：众数、中位数、分位数、均值。

(一)概念

众数是指总体中最常见的标志值，在次数分布数列中，就是出现次数最多的变量值，用表示。它主要用于测度定类数据的集中趋势，当然也适用于作为定序数据以及数值型数据集中趋势的测度值。

计算众数需要满足两个条件：一是众数只有在被研究的总体个数多时才能出现。二是被研究的总体有明显的集中趋势时才有众数。

【例4.1】某商场某日连续销售15双皮鞋的尺码组成情况如下：38，37，38，40，40，41，40，42，44，40，41，39，40，40，43出现次数最多的数是40，40就是某商场某日销售皮鞋尺码的众数。

(二)计算众数的方法

１.单项分配数列的众数计算方法

在单项分配数列中即未分组的数列中，确定众数比较容易，直接能观察出来，出现次数最多的那一组变量值就是众数。如例4.1。

1.组距分配数列的众数计算方法

在组距分配数列中即分组的数列中，根据分配数列次数最多的组确定为众数所在组，还要根据该组与前后相邻两组分配次数的关系推算众数。这种关系如下图4-1所示：

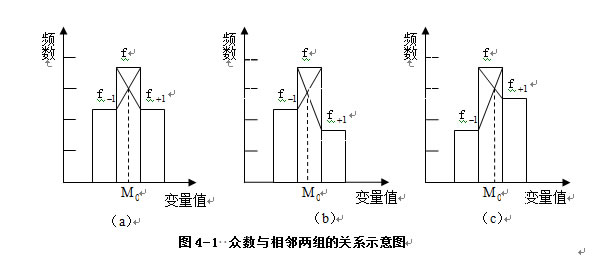
设众数组的频数为,众数前一组的频数为，众数后一组的频数为，从众数组直方图的两个顶角向相邻两组直方图的两个顶角引直线，再由交叉点向横轴引垂线，与横轴相交的点即为众数。由图4-1可以看出，当众数相邻两组的频数相等时，即，众数组的组中值即为众数的值，如图4-1（a）；当众数组前一组的频数多余众数组后一组的频数时，即，则众数会向其前一组靠，众数小于其组中值，如图4-1（b）；当众数组后一组的频数多于众数组前一组的频数时，即，则众数会向其后一组靠，众数大于其组中值，如图4-1（c）。根据这种关系，可以利用相似三角形推导出组距分配数列的众数的计算公式如下：

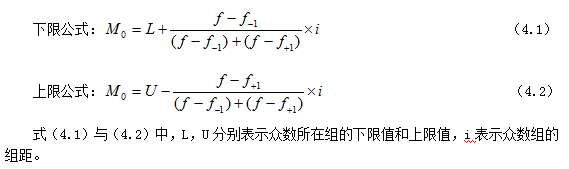
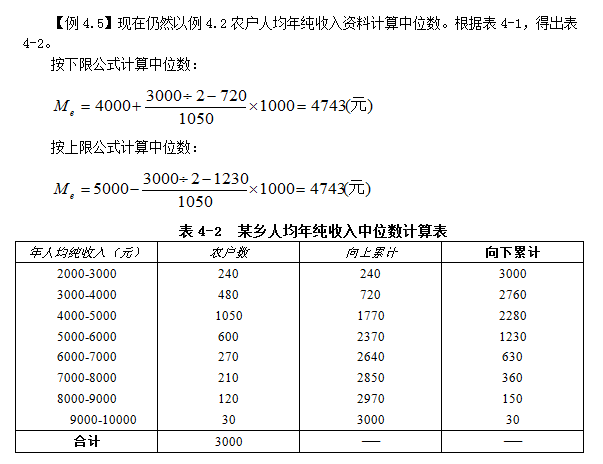
【例4.2】某乡3000农户按人均年纯收入分组的资料如表4-1，试计算其众数。

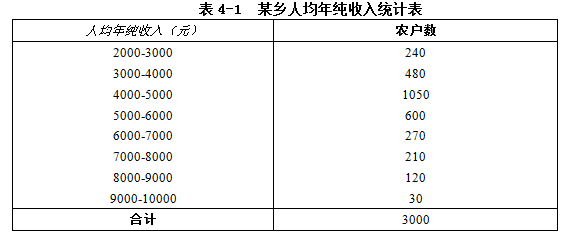
从表4-1中可以看出，众数所在的组为4000-5000，出现的最多次数为1050。

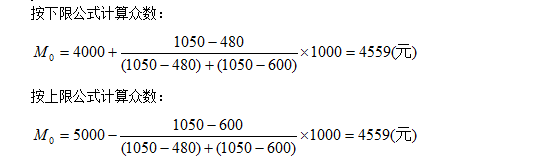
3.众数的优缺点

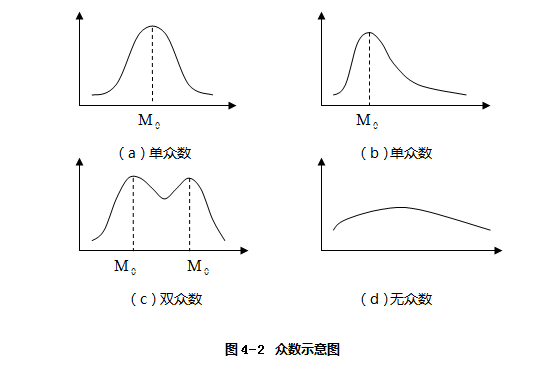
众数不受极端值的影响，较稳定，其代表性比较好。但众数仅采用中提中一部分数值计算，因而不宜用来推算总体。从分布的角度看，众数是具有明显集中趋势点的数值，一组数据分布的最高峰点所对应的数值即为众数。有的众数不一定就落在数据集合的中间区域；数列分布如果有两个最高峰点，也可以有两个众数；有些数列如果分布没有明显的集中趋势或最高峰点，众数也可能不存在。具体的示意如图4-2：

二、中位数和四分位数

（一）中位数

1.概念

中位数是指对样本数据由小到大排序后，处于中间位置上的变量值，用表示。显然，在样本中，有50％的个体小于或等于中位数，也有50％的个体大于或等于中位数。中位数是一个位置代表值，它主要用于测度定序数据的集中趋势，当然也适用于数值型数据的集中趋势，但不适用于定类数据。

2.计算中位数的方法

（1）变量值未分组情况下：

首先把n个单位的变量值按大小顺序排列，然后计算中位数所在的位次，其公式为：中位数位置=。如果总体单位数n是奇数，则居于中间位置的变量值是唯一确定的，这个位置的变量值就是中位数。如果总体单位数是偶数，则居于中间位置的变量值不是唯一确定的，应该是中间位置的两个变量值的算术平均数为中位数。即

3.中位数的优缺点

中位数的优点在于它比较容易理解，而且不受极值影响，适宜于开口组资料和某些不能用数字测定的事物，其缺点主要有灵敏度和计算功能差，对于间断数列不能计算中位数。

（二）四分位数

中位数是从中间点将全部数据分为两部分。与中位数类似的还有四分位数、十分位数、百分位数、四分位数就是对数据集合四等分的三个数值，其中的第二个四分位数即为中位数。例如某数据集合有101项数据，则第26项、51项、76项三个数据可以把数据集合分为数目相等的四个等分，这三个数就分别是第一、第二、第三四分位数，其中第一个四分位数称为上四分位数，第三个四分位数称为下四分位数，第二个四分位数就为中位数。

三、数值平均数：算术平均数、调和平均数、几何平均数

以上我们学习的众数、中位数、四分位数数据集中趋势的测度值是现对各单位变量值按一定顺序排列，然后去某一位置能够反映一般水平的代表值。而数值平均数是根据总体各单位所有变量值计算而得的平均指标，它包括算术平均数、调和平均数、几何平均数等。

（一）算术平均数

算术平均数又称均值，是全部数据的算术平均值。它在统计学中具有重要的地位，是集中趋势的最主要测度值，它主要适用于定居数据和定比数据，但不适用于数值型。其基本计算公式是：

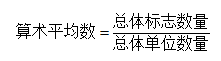
例如企业的工资总额除以职工人数求得平均工资，某县粮食总产量除以播种面积求得平均亩产量等等。
根据资料不同，计算算术平均数有简单算术平均数和加权算术平均数两种。

1.简单算术平均数

根据未经分组整理的原始数据计算算术平均值，分子是有各单位标志值即变量值简单加总的结果，因此称它为简单算术平均数。设一组数据为， 则均值的计算公式如下：

可知当我们掌握的不是各组变量值出现的频数，而是频率时，也可直接根据（4.7）式计算均值。

均值在统计学中具有重要的地位，他是进行统计分析和统计推断的基础。首先，从统计思想上看，均值是一组数据的重心所在，是数据误差相互抵消后的必然性结果。比如对同一事物进行多次测量，若所得结果不一致，可能是由于测量误差所致，也可能是其他因素的偶然影响，利用均值作为其代表制，则可以使误差相互抵消，反映出事物必然性的数量特征。其次，均值具有一些重要的数学性质：各变量值与其均值的离差之和等于零；各变量值与其均值的离差平方和最小。这些数学性质在实际中有着广泛的应用，同时也体现了均值的统计思想。

（二）调和平均数

调和平均数也称调和均值，是均值的另一种表现形式。在实际工作中，由于所获得的数据不同，有时不能直接采用均值的计算公式来计算平均数，这就需要使用调和平均数的形式进行计算。为了更好地理解调和平均数的应用场合，我们看下面的例子。

【例4.7】某蔬菜批发市场三种蔬菜的日成交数据见表4-4，计算三种蔬菜该日的平均批发价格。

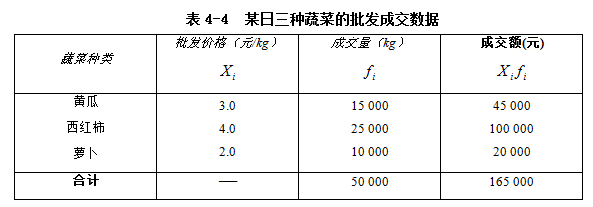
从平均价格的实际意义看，平均价格应该为成交额除以成交量。根据题中给出的数据，可以求出成交额数据，因此计算平均批发价格在形式上采用的是加权算术平均数公式，即根据式（4.6）求得结果为平均批发价格为3.3元。

如果，已知的不是成交量数据，而是成交额，就应该改变计算方法。因为此时无法直接采用式（4.6）计算加权算术平均数，这时，需要根据批发价格和成交额数据先求出成交量数据，再用成交额除以成交量即得平均价格。这一过程可以表示为：

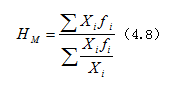
这就是调和平均数公式，式中表示调和平均数。利用此式计算平均价格同样为3.3元。这与加权算术平均数公式的计算结果完全一致。实际上，式（4.8）只是加权算术平均数的另一种表现形式。

由此可见，调和平均数实际上是算术平均数的一种变形，二者在本质上是一致的，唯一的区别就是计算时使用了不同的数据。

（三）几何平均数

几何平均数是n项变量值连乘积的n次方根。几何平均数适合于计算现象的平均比率或平均速度，反应现象增长率的平均水平。因此，凡是现象的变量值的连乘积等于总比率或总速度，都可以使用几何平均数来计算平均比率或平均速度。

1.简单几何平均数

简单几何平均数适用于计算未分组数列的平均比率或平均速度，其计算公式为：

【例4.8】 1994-1998年我国工业品的产量分别是上年的107.6%、102.5%、100.6%、102.7%、102.2%，计算这5年的平均发展速度。

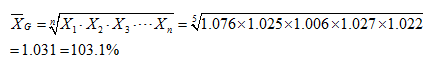
2.加权几何平均数

对于分组数列，应该采用加权几何平均数计算其平均比率或平均速度，其计算公式为：

【例4.9】某投资银行25年的年利率分别是：1年3%，4年5%，8年8%，10年10%，2年15%，求平均年利率。

• 1、计算平均指标最常用的方法和最基本的形式是（ ）【单项选择】。    
  　　 A 中位数 
  　　 B 众数
  　　 C 算术平均数
  　　 D 调和平均数
  
  教师解析：答案C.算术平均数又称均值，是全部数据的算术平均值。它在统计学中具有重要的地位，是集中趋势的最主要测度值，是最常用的方法和最基本的形式。