离散趋势反映的是各变量值远离其中心值的程度，因此也称为离中趋势，是要求出一个值来表示个案与个案之间的差异情况。这种测量法与集中趋势一起分别从两个不同的侧面描述和揭示一组数据的分布情况，与集中趋势测量法有互补的作用。资料的离散程度表明了集中趋势的代表性如何，凡离散程度愈大，则集中趋势的代表性就愈小，离散程度愈小，则集中趋势的代表性愈大。

见下例:

某三个班各选5名同学参加测试.他们的成绩分别如下

中文系:78, 79, 80, 81. 82     = 80

数学系:65, 72, 80, 88, 95      = 80

外语系:35, 78, 89, 98, 100     = 80

如果仅以集中趋势来衡量,这三个队的水平一样高,但是很明显。这80分对中文系队的同学代表性最高,而对外语系的同学代表性最低。所以还要考虑离散程度才能很好地评价这三个班同学的成绩。

常见的离散趋势统计量有异众比率,和四分位差，全距,方差及标准差。

一、异众比率

异众比率（）就是非众数的次数与全部个案数目的比率。可见异众比率是对众数的补充，异众比率越小，说明众数的代表性越好；反之，异众比率越大，则说明众数的代表性越差。公式如下：

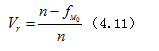
其中为众数的频数，为变量值的总频数。

【例4.9】表4-5显示了甲校学生的父亲职业统计情况，求异众比率。

表4-5  甲校学生的父亲职业统计

职业	学生人数
工人 农民 干部	152 288 110
总数	550

根据上面的表4-5，和公式（4.11）可以得到异众比率为：

二、四分位差

四分位差也称为内距或四分间距，它是上四分位数与下四分位数之差。是对定序及定序以上测量尺度的变量离散程度的测量指标。四分位差的计算方法是先将一组数据按大小排列成序，然后四等分，找出上四分位数和下四分位数，上四分位数的值（Q1）与下四分位数的值（Q3）的差异，就是四分位差（Q）。Q2就是中位值（Md），两边各有50%的个案，也就是在中位值两旁的Q1和Q3之间，共有50%的个案。因此，四分位差越大，表示有50%的个案越远离中位值，因而中位值的代表性就越小。

计算四分位差时，先求出Q1和Q3的位置，然后计算在这两个位置上的差异。Q1和Q3的位置公式是：

以下是计算四分位差的方法：

1.对原始资料

【例4.10】调查11位同学的年龄如下：17岁、18岁、18岁、19岁、19岁、20岁、20岁、21岁、21岁、22岁、22。
首先，求出Q1和Q3的位置：

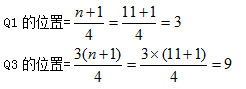
其次，从数序中找出Q1=18，Q3=21

则四分位差Q= Q3—Q1=21—18=3

2.对单值分组资料

【例4.11】如表4-6所示的学生学业成绩。

表4-6  学生的学业成绩统计

等级	学生人数向下累计 ↓        向上累计↑
甲 乙 丙 丁	5　　　　　　　　　　5　　　　　　　　　80 　　20　　　　　　　　　25　　　　　　　　　75 　　30　　　　　　　　　55　　　　　　　　　55 　　25　　　　　　　　　80　　　　　　　　　25
总数	80　　　　　　　　　-　　　　　　　　　　 -

据公式可知：

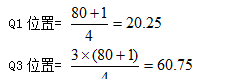
从累积次数分布表中，很易看到在这两个位置上的值分别是丁级和乙级，所以：四分位差Q=丁—乙=两个等级。

3.对组距分组资料：

对组距分组资料Q1和Q3的计算公式为：

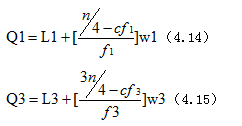
其中，L1为Q1属组之真实下限；L3为Q3属组之真实下限；f1为Q1属组之次数；f3为 Q3属组之次数；cf1为低于Q1属组下限之累积次数；cf3为低于Q3属组下限之累积次数；w1为Q1属组之组距；w3为Q3属组之组距；n为全部个案数。

【例4.12】如表4-7所示的资料

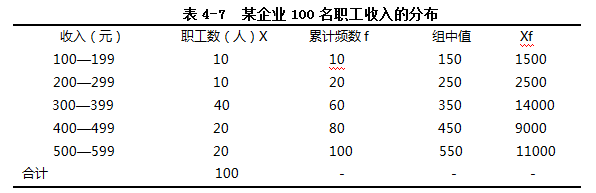
三、全距

全距又称极差，它是一组数据中最大值与最小值之差。全距是对定序及以上尺度的变量离散程度的测量。极差越小，表明资料越集中，集中趋势统计量的代表性越高。

计算全距的一般公式为：

【例4.13】某校3个系各选5名同学，参加智力竞赛，他们的成绩分别如下：

中文系：78.79.80、81.82

数学系：65.72.80、88.95

英语系：35.78.89.98.100

则三个代表队的全距分别为：中文系：82-78=4（分）数学系：95-65=30（分）英语系：100-35=65（分）

对于组距分组数据，全距也可以近似表示为：

（4.17）

全距是描述数据离散程度最简单测度值，计算简单，易于理解，但它容易受极端值的影响，个别远离群体的极值会极大改变极差，以至使它不能真实反映资料的分散程度。

四、方差及标准差

方差和标准差是衡量变异程度最常用的指标，方差通常用表示。

对于未经整理的原始数据公式为：

标准差又称均方差，方差的平方根即为标准差，通常用表示，分析定距变量的离散情况，最常用的方法是标准差。对应于公式（4.18）和公式（4.19），可以得到标准差的计算公式如下：

【例4.14】根据表4-8中1998年度和1999年度电视机广告前10名品牌广告费用统计情况，计算两个年度广告费用的标准差。

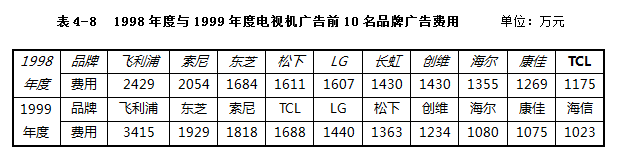
根据上表可以计算出1998年度和1999年度的平均广告费用额分别为：1604.4万元，1606.5万元。1998年度的标准差为：

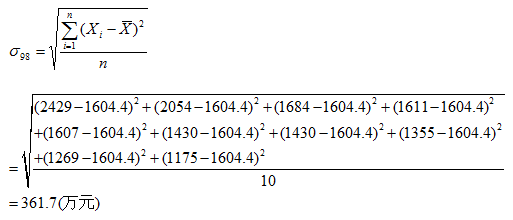
同理可以计算1999年度的标准差为674.7万元。

五、离散系数

离散系数是一种相对的离散量数统计量，它使我们能够对同一总体中的两种不同的离散量数统计量进行比较，或者对两个不同总体中的同一离散量数统计量进行比较。

离散系数是标准差与平均数的比值，用百分比表示。记离散系数为V，则公式为：

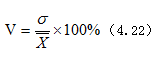
【例4.15】一项调查的结果如下，某市人均月收入为92元，标准差为17元，人均住房面积7．5平方米，标准差为1．8平方米。试比较该市人均收入和人均住房情况哪一个差异程度比较大。

由题中数据得：

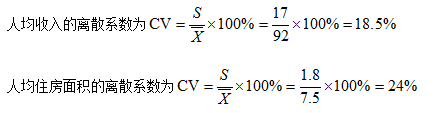
可见人均住房面积的差异情况比人均收入的差异情况要大。

以上就是常见的离散趋势统计量，离散趋势测量法与集中趋势测量法是有互补作用的。二法并用，就可以一方面知道资料的代表值，有助于估计或预测的工作，另一方面可以知道资料的差异情况，反映估计或预测时会犯的错误。但要选哪一种方法就要视乎变量的测量层次，彼此的关系可以综合如表4-9：