集中趋势和离散程度是数据分布的两个重要特征，但要全面了解数据分布的特点还需要知道数据分布的形状是否对称、偏斜的程度以及分布的扁平程度等。偏态和峰度就是对这些分布特征的进一步描述。

一、分布偏态的测度

偏态是对分布偏斜方向和程度的测度。有些变量值出现的次数往往是非对称型的，如收入分配、市场占有份额、资源配置等。变量分组后，总体中各个体在不同的分组变量值下分布并不均匀对称，而呈现出偏斜的分布状况，统计上将其称为偏态分布。

利用众数、中位数和平均数之间的关系就可以判断分布是对称、左偏还是右偏，但要测度偏斜的程度则需要计算偏态系数。统计分析中测定偏态系数的方法很多，一般采用矩的概念计算，其计算公式为三阶中心矩与标准差的三次方之比。具体公式如下：

从公式（4.23）可以看到，它是离差三次方的平均数再除以标准差的三次方。当分布对称时，离差三次方后正负离差可以相互抵消，因而的分子等于0，则=0；当分布不对称时，正负离差不能抵消，就形成了正与负的偏态系数。当为正值时，表示正偏离差值较大，可以判断为正偏或右偏；反之，为负值时，表示负偏离差值较大，可以判断为负偏或左偏。

偏态系数的数值一般在0与±3之间，越接近0，分布的偏斜度越小；越接近±3，分布的偏斜度越大。

【例4.16】某管理局所属30个企业2005年3月份利润额统计资料如表4-10所示，要求计算该变量数列的偏斜状况。

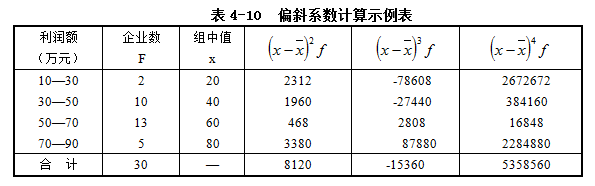
利用表4-10中有关数据计算标准差如下：

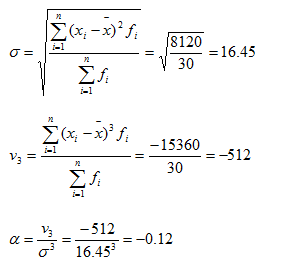
计算结果表明该管理局所属企业利润额的分布状况呈轻微负偏分布。

二、分布峰度的测度

峰度是分布集中趋势高峰的形状。在变量数列的分布特征中，常常以正态分布为标准，观察变量数列分布曲线顶峰的尖平程度，统计上称之为峰度测度。如果分布的形状比正态分布更高更瘦，则称为尖峰分布，见图4-3（a）；如果分布的形状比正态分布更矮更胖，则称为平峰分布，见图4-3（b）。

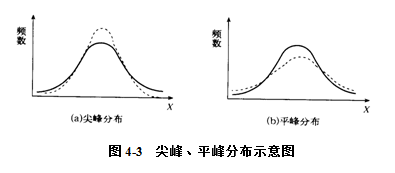
测度峰度的方法，一般采用矩的概念计算，即运用四阶中心矩与标准差的四次方对比，以此来判断各分布曲线峰度的尖平程度。公式如下：

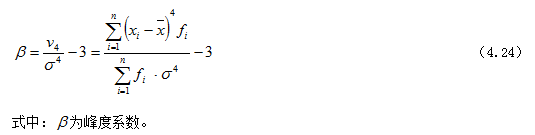
峰度系数是统计中描述次数分布状态的又一个重要特征值，用以测定邻近数值周围变量值分布的集中或分散程度。它以四阶中心矩为测量标准，除以是为了消除单位量纲的影响，而得到以无名数表示的相对数形式，以便在不同的分布曲线之间进行比较。由于正态分布的峰度系数为0，当＞0时为尖峰分布，当＜0时为平顶分布。

【例4.17】继续例4.16，要求计算该变量数列的峰度。

根据表4.9中有关数据计算峰度系数如下：

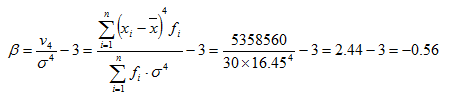
计算结果表明，上述企业间利润额的分布呈平顶峰度，各变量值分布较为均匀。