当前位置:课程学习>>第五章 时间数列统计分析>>学习内容>>知识点二
知识点二:时间数列的水平分析
○ 教师解析
一、发展水平
发展水平是指时间数列中的每一项具体指标数值,它反映了某种社会经济现象在不同时间上所达到的水平,也是计算各项时间分析指标的基础。发展水平一般是时期或时点总量指标,如销售额、在册工人数等;也可以是平均指标,如:平均工资、单位产品成本等; 还可以是相对指标,如:计划完成程度、商品流转次数等。
在时间数列中,由于发展水平所处的位置不同,有最初水平和最末水平。最初水平是指时间数列中第一项指标数值,它表示事物发展的原有基础;最末水平是指最后一项指标,它表示事物发展的在一定时期内的最终结果。可用符号表示![]() 它们代表数列中各个发展水平。其中
它们代表数列中各个发展水平。其中![]() 就是最初水平,
就是最初水平,![]() 是最末水平,其余的就是中间各项水平,简称为中间水平。
是最末水平,其余的就是中间各项水平,简称为中间水平。
为了计算时间分析指标,需要将不同时间的发展水平进行比较。对比时把所要研究的那个时期(时点)的发展水平叫做报告期发展水平(或计算期水平),简称报告期水平;把用来作为对比基础时期(时点)的发展水平叫做基期发展水平,简称基期水平。报告期水平和基期水平不是固定不变的。它根据研究目的的不同和时间的变更而改变。
二、平均发展水平
平均发展水平又称之为序时平均数,它是将整个时间数列作为一个整体,反映这个整体的一般水平。序时平均数与一般的算术平均数虽然都是通过具体数值计算,反映整体的一般水平,但两者也存在着明显的差异,主要表现在:
(一)序时平均数平均的是事物在不同时间上的数量差异;算术平均数平均的是总体各单位某一数量标志在同一时间上的数量差异。
(二)序时平均数是从动态上说明某一事物在不同时间上发展的一般水平;算术平均数是从静态上说明同一事物总体不同单位在同一时间上的一般水平。
(三)序时平均数是根据时间数列计算的;算术平均数是根据变量数列计算的。
1.根据绝对数时间数列计算序时平均数
由前述可知,在绝对数时间数列中主要是由总量指标所构成的时间数列,而总量指标根据其时间状况不同又可分为时期指标与时点指标,并分别构成时期数列与时点数列。时期数列与时点数列各自所具有的不同特点,使得在平均指标的计算上具有明显的差异。
(1)由时期数列计算序时平均数
由于时期数列中的各项指标数值都是反映社会经济现象在一定时期内的过程总量,具有可加性,因此我们可以采用简单算术平均的方法计算序时平均数,即将时期数列中研究范围内的各项指标数值之和除以时期项数来得到。计算公式为:

【例5.1】已知某企业一季度产值为500万元,二季度产值为720万元,三季度产值为900万元,四季度产值为1140万元,计算该企业全年平均季度产值;
全年平均季度产值=(500+720+900+1140)/4=815(万元)
(2)时点数列序时平均数
要精确计算时点数列序时平均数就应该有每一瞬间都登记的资料。这在实际中几乎是不可能的,所以习惯上以天为单位作为瞬间即一时点。即使这样也较繁杂。通常的作法有两种:一是每隔一段时间登记一次,时点定在月(季、年)初或末,每次登记的间隔相等;二是只当现象的数量发生变化时登记,每次登记的间隔不等。两种情况下计算序时平均数的方法有所不同:(1)连续时点数列计算序时平均数

例如表5-5某专业学生星期一至星期五出勤人数资料如下表:

计算该专业学生平均每天出勤人数。
由于是连续时点数列平均数的计算,故用计算公式(5.2)可得:
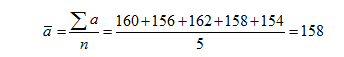
由计算可知,该专业学生本星期平均每天出勤人数为158人
根据这个思路,对于不连续但间隔相等的时间数列![]() 其序时平均值就是各期期初发展水平与期末发展水平的算术平均数之后再进行算术平均,即:“首尾折半法”
其序时平均值就是各期期初发展水平与期末发展水平的算术平均数之后再进行算术平均,即:“首尾折半法”

【例5.2】某企业2005年有关月的月初职工人数是:1月1日为240人;4月1日为240 人;7月1日为260人;10月1日为250人;12月31日为260人,要求确定2005年职工平均人数:
由于登记的时间间隔都为三个月,故根据公式(5.3),得
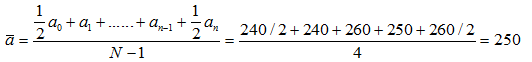
(3)连续时点数列计算序时平均数
在某些情况下,间断时点数列的间隔也可能是不相等的。如果掌握间隔不等的每期期末资料,则可用各间隔时间为权数对各项相应的相邻两时点数列加权,应用加权算术平均法计算序时平均数。其计算公式为:
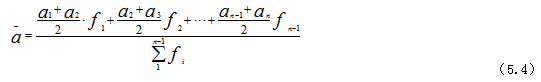
式中:f 表示时间间隔长度,a表示各指标值。
【例5.3】某商场2002年库存情况 如下表所示。计算该商场2002年的月平均库存额。

(4)相对数和平均数列时平均数的计算
从形式上看,无论是相对数还是平均数,都是两个直接对比的结果,因此相对数时间序列与平均数时间数列的序时平均数的计算原理相同。
对于一个动态数列![]() c
c![]() ,
,![]() c
c![]() ,…,c
,…,c![]() ,其分子指标 a 的时间数列是a
,其分子指标 a 的时间数列是a![]() ,a
,a![]() ,…,a
,…,a![]() ,其分子指标 b 的时间数列是b
,其分子指标 b 的时间数列是b![]() ,b
,b![]() ,…,b
,…,b![]() ,则
,则![]() c
c![]() ,c
,c![]() …c
…c![]() 的序时平均基本公式是:
的序时平均基本公式是:
![]()
式中“=”左边代表相对指标或平均指标的序时平均数,右边分子、分母分别代表子项和母项总量指标的序时平均数。在这里a、b作为总量指标时间数列(时点或时期)有三种可能:
①a、b均为时期数列。
②a、b均为时点数列。
③a、b一个为时点数列一个为时期数列。
总之,相对数或平均数时间数列的序时平均数计算其关键是搞清楚这一相对数或平均数的分子分母指标内容与性质。
【例5.4】某商业企业2005年各季商品销售及季初库存资料如表所示,其中,第四季末库存额为2万元,计算全年平均每季的商品流转次数和平均每季的流通费用率。
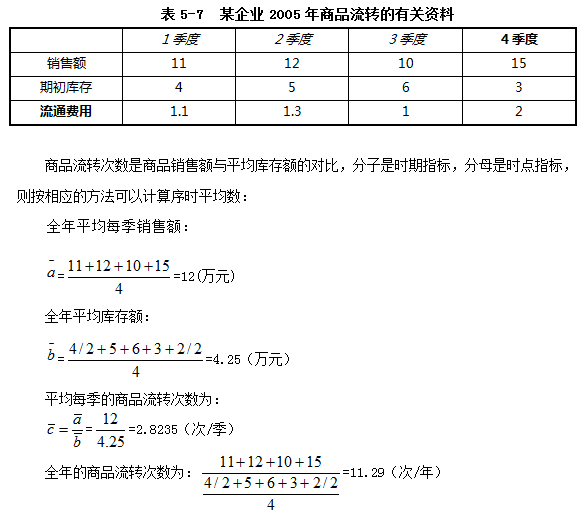
三、增长量指标
(一)增长量的含义
时间数列反映了一个现象的动态过程,因此通过数量对比便可以分析现象数量上变化的程度。增长量指标是反映现象数量变动的常用指标,它是指某种社会经济现象在一定时期内增长或减少的绝对数量。它等于报告期水平与基期水平之差。其计算公式为:
增长量=报告期水平–基期水平 (5.6)
(二)增长量的种类
由于对比的基期不同,增长量有逐期增长量(也称“环比增长量”)和累计增长量(也称“定基增长量”)两种,逐期增长量是两个相邻时期发展水平之差,即:逐期增长量=报告期水平-前一期水平
累计增长量是表示某种社会现象在一定时期内(从固定基期到报告期)累积增长的总量。其计算公式为:累积增长量=报告期水平-某一固定基期水平
用公式表示即为:逐期增长量=a1-a0,a2-a1,……,an-an-1
累计增长量=a1-a0,a2-a0,……,an-a0
我们不难得出如下结论:
1.累计增量等于逐期增量之和,即:
(a1-a0)+( a2-a1)+……+(an-an-1)= an-a0
2.相邻两期累计增长量之差等于相应的逐期增量
在实际统计分析工作中,为了消除季节变动的影响,增加可比性,常计算本期发展水平与上年同期水平的增减数量,称为年距增长量。
3.平均增长量指标
由以上可知,逐期增长量构成了一个时间数列,由于每一期增量有多有少,我们可以用“平均增长量”来刻画增量序列的一般水平。我们用平均增长量说明现象在一定时期内平均每期增长的数量。用公式表示:
平均增长量=逐期增长量之和/逐期增长量个数
用符号表示为:
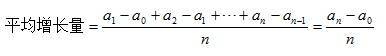
○ 边学边练
- 1、根据时期指标时间数列,计算平均发展水平采用( )?【单项选择】
A 加权算术平均法
B 首末折半法
C 几何平均法
D 简单算数平均法
