一、影响因素及其分解模型

(一)因素的确定

事物的发展变化同时受多种因素的影响，在诸多影响因素中，有些对事物的发展起着长期的、决定性的作用，致使事物的发展呈现出某些趋势和一定的规律性，各类事物普遍存在的影响因素，构成动态数列的共有因素，按它们的性质和作用，可以归纳为长期趋势、季节变动、循环变动和随机变动四种。每一动态数列都是由这些因素的全部或部分构成的。动态数列的因素分析任务就是要正确确定动态数列性质，对构成动态数列各种因素加以分解，再分别测定其对动态数列变动的影响。

1.长期趋势(以T表示)：长期趋势是指由于某种本质因素的影响，现象在相当长的时间内，呈现的持续上升或下降的发展势态。它是现象在一段时间内发展变化的规律性表现，是动态数列分析的重点。

例如：由于生产力水平的提高，世界各国的国民收入和人均所得有逐年上升的趋势。若用图形表现，可得一趋势线。若趋势线为直线，则称为直线趋势；若趋势线为曲线，则根据其曲线形式称为某种曲线趋势，如二次曲线趋势，指数曲线趋势等。

2.季节变动(以S表示)：季节变动是指动态数列受自然因素和社会因素影响而发生的有规律的周期性波动。季节变动的周期通常为一年。

如在商业活动中，我们经常听到“销售旺季”或销售淡季”，在旅游业中，我们也常常使用“旅游旺季”或“旅游淡季”这类述语，等等。这些述语表明，这些活动因季节的不同而发生着变化。

3.循环变动(以C表示)：循环变动是指现象以若干年为一周期，近乎规律性从低至高再从高至低的周而复始变动。循环波动不同于趋势变动，它不是朝着单一方向的持续运动。而是涨落相间的交替波动。如经济危机就是循环变动，每一循环周期都要经历危机、萧条、复苏和高涨四个阶段。

4.随机变动(以I表示)：随机变动亦称不规则变动或剩余变动，是动态数列除了上述三种变动之外剩余的一种变动，是偶然因素引起的一种随机波动。

如自然灾害、战争等无法预见的因素引起的波动。随机变动与时间无关，是一种无规律的变动，难以测定，一般作为误差项处理。

（1）因素的构成模型

按上述四种变动因素对动态数列的影响方式不同，动态数列可以形成多种模型，称为动态数列因素构成模型。按对四种变动因素相互关系的不同假设，可形成乘法模型、加法模型和乘加模型等。

1.乘法模型；Yt＝Tt×St×Ct×It

2.加法模型：Yt＝Tt＋St＋Ct＋It

3.乘加模型：Yt＝Tt×St＋Ct×It。

式中Yt为动态数列在t期发展水平, Tt、St、Ct、It分别表示t 期的趋势值、季节变差、循环变差、不规则变差。

如果四种变动因素之间存在着相互交错影响关系，宜选乘法模型；如果四种变动因素是相互独立的，各构成因素的数量值可以相加，宜选用加法模型；如果存在其他情况，则需具体分析。在现实中普遍运用的是乘法模型，所以在这一部分主要讲解乘法模型。

二、长期趋势的测定

长期趋势的测定模型是根据现象的趋势形态确定的，既有直线模型，也有非直线模型。测定的方法很多，这里着重介绍移动平均法和线性最小二乘法两种。

（一）移动平均法

移动平均法是对原动态数列逐项求序时平均数，平均的项数固定，并逐项移动得出由这些平均数构成的新数列，它可以消除某些周期因素及随机因素的影响，显示出现象的长期趋势。使用移动平均法应注意下列问题：

1.修匀(移动平均)后的动态数列会损失一部分信息量。修匀(移动平均)后的动态数列的项数减少了,并且所选时间跨度越大，减少项数越多。如用五项移动平均，首尾各少两项；六项移动平均，首尾各少三项数字。可见，得到的移动平均趋势值减少，会损失一部分信息量。

2.平均的项数（时间跨度）应以现象发展变化的周期长度或周期长度的倍数为准，以消除周期因素的影响。时间跨度一般选为奇数。采用奇数平均,一次就能得到移动平均趋势值。如需要移动两次才能得到移动平均趋势值，这时移动平均显现长期趋势的效果较好。但时间跨度较小，修匀效果则较差。

【例5.5】据某铁路局货物周转量资料，运用移动平均法，测定长期趋势。具体步骤见表5-9。

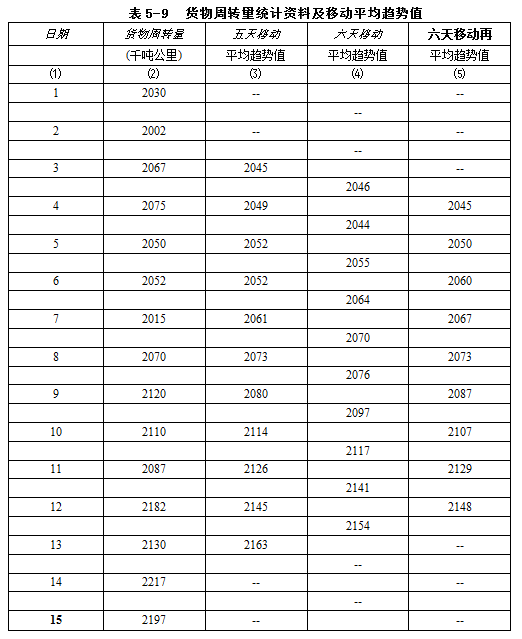
如果五天平均移动，则把日期1.2.3.4.5五天的货物周转量相加再除以5，作为日期3的“趋势值”，依次类推。

从表5-9知,移动平均的结果为（3）和（5）栏，明显看出周转量的上升趋势。

（二）应用最小二乘法

对动态数列采用最小二乘法配合趋势直线，是趋势测定最常用方法：

设Yt=a+bt为趋势方程，t为时间变量，时间变量可设为自然数也可将时间变量调整为正负相对应的等距整数数列,使∑t=0，则可以简化计算过程。方程中的参数求解公式为：

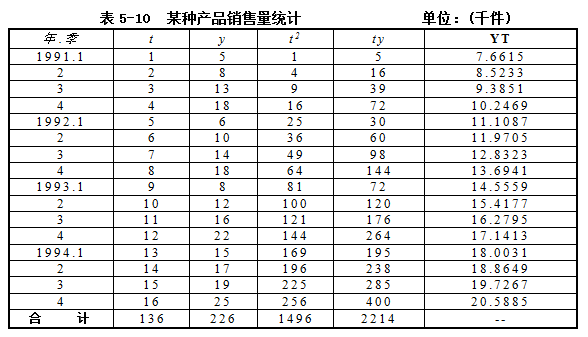
将表5-10中有关数据代入趋势方程的参数求解公式得：a=6.7997；b=0.8618

则直线趋势方程为：Yt＝6.7997+0.8618t

运用已估计出参数的趋势方程，求出趋势方程所确定的各期趋势值所构成的新数列。将这些趋势值描绘在图上便形成一条上升的趋势线。这是一条趋势值与数列原值的离差平方和为最小的趋势线。

三、周期因素的测定

（一）季节变动的测定

在按月或按季编制的时间序列中，往往存在着一种随季节周而复始的周期性变动。季节变动的测定，就是测定各月(季)的季节比率，说明季节变动的一般规律。

季节变动的测定作用：通过对现象季节变动的分析和研究，可以根据现象过去的季节变化规律，以作为当前生产经营活动的依据。

比如，对一个公司销售活动的研究，可以分为其销售额的变动是季节因素的影响所致，还是由于经营手段或其它偶然因素的影响，从而制定出有效的经营策略。

测定季节变动的方法：直接季节比率测算法和移动平均趋势剔除法。前者不考虑长期趋势等因素对季节的影响；后者则考虑长期趋势等因素的影响，且先剔除长期趋势等因素的影响，再求季节变动的比率。

1.直接季节比率测算法：直接季节比率测算法的基本思想：计算出各年同月（季）的平均数，以消除随机影响，作为该月的代表值；然后计算出总月（季）的平均数，作为全年的代表值；再将同月（季）平均数与总月（季）平均数进行对比，即为季节指数。具体来说，直接季节比率测算法是：（1）先将各年同月(季)数值列在同一栏内；（2）求各年同月(季)的平均数；（3）求各年同月(季)平均数对全期各月(季)总平均数的比率，即季节比率：季节比率＝（各月(季)平均数/全期各月(季)总平均数）×100%

注意：这里，四个季节比率之和应等于400%(使用月份资料时,十二个季节比率之和应等于1200%)。有时，因舍入误差使季节比率之和不等于400%(1200%)，就需要把差额分摊到各季(月)的季节比率上。

调整季节指数的算法为：（1）计算各季节指数的平均数；（2）用各季节指数除季节指数的平均数，即得调整后的相应各期季节指数。

【例5.6】用表5-10资料，直接计算季节比率如表5-11所示。

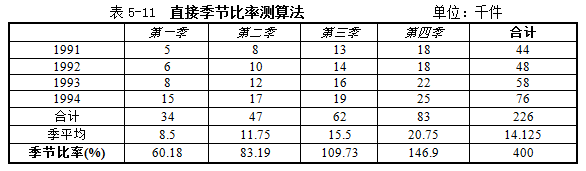
有了季节比率，就可知该商品销售量按季节变化的信息，第一季度最低为60.18%，第二季度略低，第三、四季度大幅度上升，其中第四季度最高为146.67%，可认为三、四季度为旺季，一、二季度为淡季。

2.趋势剔除法：趋势剔除法的基本思想：由于长期趋势等非季节性因素的存在,因此，需把测定好的非季节性因素值从原数列中剔除去，然后再求季节变动。以得到没有长期趋势等因素影响的季节比率。

趋势剔法解决问题的具体步骤：

根据时间序列的数据求出各期的趋势值Vt 。求趋势值可以用移动平均法也可以用最小二乘法。将时间序列的实际观察值Yt除以趋势Vt,得到各个月的季节指数，由于它们是利用样本数据直接求得，故也称为样本季节指数。样本季节指数中不可避免地包含不规则变动，它只能反映在特定的某月（或季）由于季节变动和不规则变动所造成的高于或低于趋势值的比率，即：

Y=T*S*I

Y/T=S*I

为了反映季节变动所造成的影响，应消除不规则变动。

（1）将计算得到的各年同月样本数据指数进行简单算术平均，即可得到理论季节指数。它已经不包含不规则的变动，而反映序列季节变动的一般规律。

上面的步骤也可以用下面的式子表示

Yt/Vt=ft

ft=(fi +fi+T +．．．+f(m-1)T+i)/m     i=1,2,．．．T        (5.18)

式中：ft表示理论季节指数；fi样本季节指数；T表示季节周期的长度；m表示时间序列数据所包含的年数。

注意：理论季节指数的平均值应为1，若遇到均值不是1的情况，应对其进行调整。调整的方法为：求出各理论季节指数的平均数，拿各理论季节指数除各季节指数的平均数。下面是一平均趋势变动剔除法的例子，即趋势线由移动平均法求得。

根据表5-12市水产品的销售量(y)资料来具体说明移动平均趋势剔除法的方法与步骤。

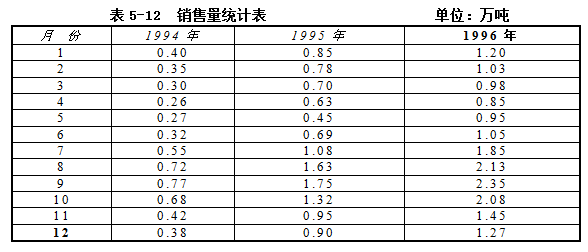
将表5-12数列进行12项移动平均，可消除季节因素的变动，得到非季节因素(TC)，见表5-13。

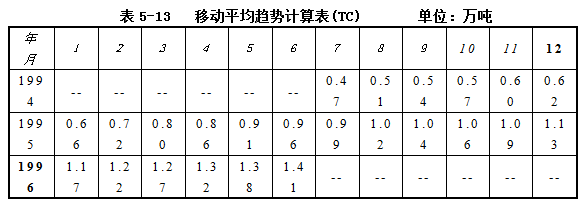
将趋势值等非季节因素剔除。计算三年内各月份实际销售量和修匀值的比率(Y/TC)，如1994年7月为0.55/0.47=117%。列表5-14如下：

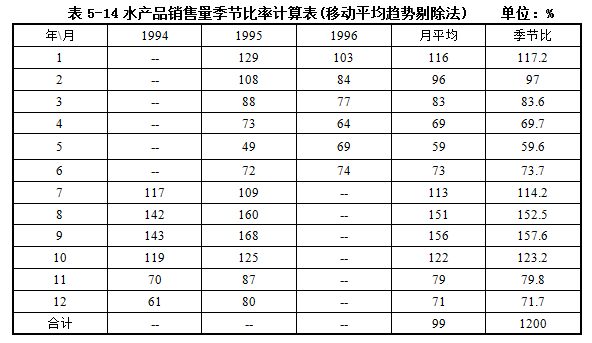
对剔除长期趋势等因素后的数列求季节比率，得到单独的季节比率。将这些比率绘成曲线图，可直观地观察季节变动规律。我们进行动态分析。从表5-14最末一行可知,某市水产品销售量1月、7月、8月、9月、10月份为旺季，其余月份为淡季。

（二）循环变动的测定

分析循环波动的主要目的：探索现象活动的规律性，研究不同现象之间循环波动的内存联系，为经营管理的预测和决策提供客观依据。

测定循环变动的两种方法：即剩余法和直接法。

1.剩余法

剩余法是从动态数列中分别消除长期趋势、季节变动和不规则变动，其剩余的结果便是循环变动。按照关系式：

Y=T*S*C*I               　　　　　  (5.19)

消除消除长期趋势、季节变动和不规则变动的两种方法。

第一，分别求得季节变动和长期趋势值，并把两者消除。即

Y/(T·S)＝（T·S·C·I）÷(T·S)＝C·I    　　　　 (5.20)

将CI数列进行移动平均修匀，得到各期循环变动系数，就达到测定循环变动的目的。

第二，先对Y采用季节长度作移动平均,以消除季节变动和不规则变动，移动平均的结果便形成了长期趋势与循环波动共存的TC数列,然后再从TC中剔除最小二乘趋势值,便求得循环波动值TC/T=C。

2.直接法

直接法的基本思路：通过计算动态数列的年距发展速度，来消除长期趋势和季节变动；再采用移动平均法,消除年距发展速度中的不规则变动因素，最后得出循环变动。

若时间数列为年度资料，可将“直接法”变通为“环比法”，即计算环比发展速度，而后采用移动平均法消除环比发展速度中的不规则变动因素，得到循环变动。

具体做法：用每年各月数值与上年同月数值之比，求得循环和不规则变动相对数，来反映现象循环波动的方法。其计算公式为

C·I＝Yt,i/Yt-1,I             (5.21)

其中：i＝1,2,…12或1,2,3,4；C·I为第t年第i月的循环和不规则变动相对数；Yt,i为第t年第i月的时间数列数值。