当前位置：课程学习>>第六章 假设检验>>学习内容>>知识点二
知识点二：方差已知情况下对总体均值的假设
双侧检验
某运动设备制造厂生产一种新的人造钓鱼线，其平均切断力为8kg，标准差为0.5kg，如果有50条随机样本进行检验，测得其平均切断力为7.8kg试检验假设总体均值是否为8kg。（取显著性水平为0.01）
○ 教师解析
本题是已知方差，检验均值是否等于8kg的问题.因为有50条样本，比较大，因此总体可近似为正态分布
题中待检验假设为
在H0成立条件下，选检验统计量
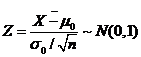
对给定正数：
这里
得其临界值为2.575；由样本数据，得均值为7.8，样本容量为50，标准差为0.5。算得Z统计量值为:
由于：
样本落入拒绝域
决策：在0.01水平上拒绝原假设
结论：有证据表明平均切断力不等于8kg
左侧检验
某批发商欲从生产厂家购进一批灯泡，根据合同规定，灯泡的使用寿命平均不能低于1000小时。已知灯泡使用寿命服从正态分布，标准差为20小时。在总体中随机抽取100只灯泡，测得样本均值为960小时。批发商是否应该购买这批灯泡？(a＝0.05)
○ 教师解析
首先设立原假设和备择假设：
样本容量为 n=100
由于a＝0.05，所以临界值为-1.645，显然z值绝对值大于临界值
决策:在 a = 0.05的水平上拒绝H0
结论:有证据表明这批灯泡的使用寿命低于1000小时
右侧检验
根据过去大量资料，某厂生产的电子元件的使用寿命服从正态分布N~(1020，1002)。现从最近生产的一批产品中随机抽取16只，测得样本平均寿命为1080小时。试在0.05的显著性水平下判断这批产品的使用寿命是否有显著提高？(a＝0.05)
○ 教师解析
首先建立原假设和备择假设：
计算检验统计量：
由于a＝0.05，所以临界值为1.645，显然z值绝对值大于临界值
决策：在 a = 0.05的水平上拒绝H0
结论：有证据表明这批电子元件的使用寿命有显著提高
通过对上述案例的学习，你是否掌握了方差已知情况下对总体均值的假设的相关知识，接下来我们进入总结与反思。
