一、σ2未知条件下总体均值检验

设总体服从正态分布，其方差未知:

（1）检验假设

则利用的统计量为

故选取T作为检验统计量,记其观察值为t，相应的检验法称为t检验法。

由于样本均值是总体均值的无偏估计量,样本方差是总体方差的无偏估计量,当H0成立时,t绝对值不应太大, 当H1成立时,t绝对值有偏大的趋势,对于给定的显著性水平,查分布表使：

由此即得拒绝域为

根据一次抽样后得到的样本观察值X1，X2，…，Xn，计算出T的观察值t,若

则拒绝原假设H0,即认为总体均值与检验值有显著差异；若

则接受原假设H0,即认为总体均值与检验值无显著差异。

类似地，对单侧检验有：

(2)右侧检验：检验假设

可得拒绝域为：

(3)左侧检验：检验假设

可得拒绝域为：

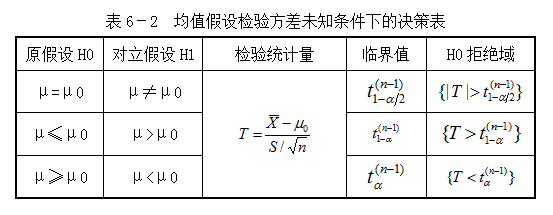
将上述各种结果，列表显示如下。