一、假设检验的步骤及有关概念

(一)统计假设和假设检验

统计假设：就是对总体的分布类型或分布中某些未知参数作某种假设，然后由抽取的子样所提供的信息对假设的正确性进行判断的过程。总体参数包括总体均值、比例、方差等。

假设检验：是事先对总体参数的数值提出某种假设，然后利用样本所提供的信息检验假设是否成立的过程。特点是采用逻辑上的反证法和依据统计上的小概率原理，现以实例说明。

对总体分布的数字特征(或参数)作出待检假设H0，然后根据从总体中抽取的一个样本对H0是否为真作出推断，像这样的一个过程称为统计假设检验，简称假设检验，在假设检验中，希望通过研究来加以证实的假设，常作为备择假设，用H1表示。而H1的对立面称为零假设或待检假设，用H0表示。

（二）基本思想

小概率事件在一次试验中可以认为是几乎不可能发生的。为了检验一个假设H0是否成立,我们先假设H0是成立的,如果根据这个假定，导致一个小概率事件的发生，从而说明原来的假设H0是不正确的，因此我们拒绝假设H0，如果没有由此而导出不合理的结果，我们则不能拒绝H0，即接受假设H0，与H0相对的假设称为被择假设。用H1表示。

（三）检验的方法

这个判断写在备择假设H1中，H0是其相对立的判断，怎样写H0和H1呢，根据问题的提出是否有倾向性或问题陈述中对被检验对象的最高要求或最低要求，建立两个相对立的结论，然后看哪一结论有等号，那么有等号的这一结论就是H0，我们要检验的是H1，假设此结论不成立，那么就有H0成立（使用H0中有等号的部分）,在H0成立的条件下就是我们需要的分布，把样本数据代入就成统计量，它应满足概率为的随机事件，倘若把代入分布中，统计量不满足概率为的随机事件，而是满足概率为的事件，于是此假设不正确，而备择假设H1成立。检验方法的反证法和一般的反证法不同之处有两点，第一此反证法依赖于概率的大小，改变概率（检验水平）的大小，可能会改变结论，第二此反证法无论证明的不等式成立不成立都会有一种判断。

（四）检验水平的含义

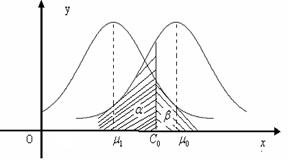
设有两个总体，一个是高三合格的学生，期望值为。另一个总体是高三不合格的学生，期望为，在高考一次性考试中有这样一部分学生本来是属于合格总体，但因分数不达录取线而被淘汰，这部分学生的数目占全体合格学生的，称这部分为弃真部分。称α为弃真概率。另有一部分学生本来属于不合格总体，但因为高考发挥的好达到录取分数线，而被录取，这部分学生占不合格总体的，称这部分为存伪部分，称β为存伪概率，α、β不能同时缩小或扩大，只能根据问题的实际意义调整它们，作为药品的合格率，宁可放大α使弃真的部分多一些，也不能让假药混进来。高考录取宁可放大β值，使不合格的学生混进来也不能把合格的学生抛弃了，关于α、β更深的理论可以参阅下文。

（五）和区间估计的关系

在假设检验中接受H0，相当于区间估计中落在估计区间内，如在水平下方差已知时，当时接受H0，相当于包含总体均值，并有一定的概率保证程度。

（六）假设检验的基本步骤

1．根据实际问题提出原假设H0及备择假设H1

2．构造一个合适的检验统计T或者Z统计量等

3．对于给定的检验水平a，查表确定分位数(临界值)λ

4．由样本值x1,x2,…,xn计算统计量之值T

5．将T或者Z与临界值比较，作出判断，以T双侧检验为：

当|T|>Ta/2 (或T>Ta/2或T<Ta/2)时，小概率事件发生就拒绝H0，否则就接受H0。这里所说的小概率事件的概率就是检验水平a，通常取a=0.05，0.01。根据上面的讨论，我们按小概率原则确定H0的拒绝域而达到检验H0的目的是有些武断，可能犯两类错误。

二、假设检验的两类错误

在统计的假设检验中，对原假设或被择假设所作出的判断，都是根据样本所含的信息做出的，由于抽样具有随机性，这样作出的判断就不可避免的要犯错误，所犯的错误有两类：

第一类错误：当原假设H0为真时，而我们根据抽样的结果错误地拒绝了H0，有时也称此为弃真错误。犯第一类错误的概率为

第二类错误：当H0不真(H1为真)时，判断结果却接受了H0，这种错误也称纳伪错误。犯第二类错误的概率为

α与β之间一般没有明确的解析关系。一个优良的假设检验准则应该使犯两类错误的概率均尽可能小。但一般说来，当样本容量给定时，犯两类错误的概率不能同时减小，若减小其中之一，另一个往往就会增加。要同时减小犯两类错误的概率，通常的方法就是增加样本容量。

因此在实际应用中，当样本容量给定时，我们一般只对犯第一类错误的概率加以控制，使它小于或的等于事先给定的α，我们称此为显著性水平，这种只对犯第一类错误的概率加以控制，而不考虑犯第二类错误的概率的统计检验问题，我们称之为显著性检验问题。

三、假设检验的类型：双边检验与单边检验

在备择假设H1：中，可能大于，也可能小于，称H1为双边备择假设，相应的检验称为双边检验。不论是拒绝H0还是接受H0，我们都必需采取相应的行动措施。

例如，某种零件的尺寸，要求其平均长度为10厘米，大于或小于10厘米均属于不合格。

提出原假设: H0:  = 4

提出备择假设: H1: ≠ 4

如果对假设H0：，H1：，进行检验称为右边检验。

例如，采用新技术生产后，将会使产品的使用寿命明显延长到1500小时以上。

建立的原假设与备择假设应为：

H0：1500

H1：1500

如果对假设H0：，H1：，进行检验称为左边检验。

例如，改进生产工艺后，会使产品的废品率降低到2%以下。建立的原假设与备择假设应为：

H0：≥2%

H1：<2%

本质上，也就是拒绝域在双边（侧）的称为双侧检验；拒绝域在右边（侧）的称为右边（侧）检验；拒绝域在左边（侧）的称为左边（侧）检验 。