一、方差分析的内容

（一）方差分析中的常用术语

1.因素（Factor）

因素是指所要研究的变量，它可能对因变量产生影响。一个是因素，因素是一个独立的变量，是方差分析研究的对象。要分析不同销售方式对销售量是否有影响，所以，销售量是因变量，而销售方式是可能影响销售量的因素。

2.水平（Level）

因素中的内容称为水平。水平指因素的具体表现，如销售的四种方式就是因素的不同取值等级。有时水平是人为划分的，比如质量被评定为好、中、差。

3.单元（Cell）

单元指因素水平之间的组合。如销售方式一下有五种不同的销售业绩，就是五个单元。方差分析要求的方差齐就是指的各个单元间的方差齐性。

4.元素（Element）

元素指用于测量因变量的最小单位。一个单元里可以只有一个元素，也可以有多个元素。

5.均衡（Balance）

如果一个试验设计中任一因素各水平在所有单元格中出现的次数相同，且每个单元格内的元素数相同，则称该试验是为均衡，否则，就被称为不均衡。不均衡试验中获得的数据在分析时较为复杂。

6.交互作用（Interaction）

如果一个因素的效应大小在另一个因素不同水平下明显不同，则称为两因素间存在交互作用。当存在交互作用时，单纯研究某个因素的作用是没有意义的，必须分另一个因素的不同水平研究该因素的作用大小。如果所有单元格内都至多只有一个元素，则交互作用无法测出。

（二）用方差分析来检验假设有三个假定

1.各个水平的观察数据必须服从正态分布：在水平Ａi下的数据是来自正态总体的一个样本，i=1,2…,r。即对于因素的每一个水平，其观察值是来自服从正态分布总体的简单随机样本，比如，每个行业被投诉的次数必需服从正态分布。

2.方差相同或者叫方差齐性：r个正态总体的方差相等，即：

各组观察数据是从具有相同方差的总体中抽取的，比如，四个行业被投诉次数的方差都相等。

3.随机性：所有数据Yij都相互独立。比如，每个行业被投诉的次数与其他行业被投诉的次数独立。

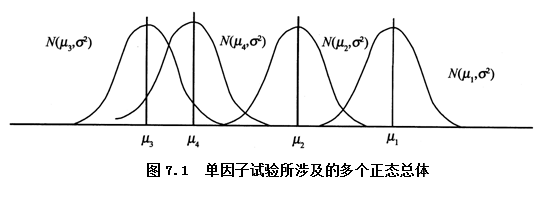
二、方差分析的原理

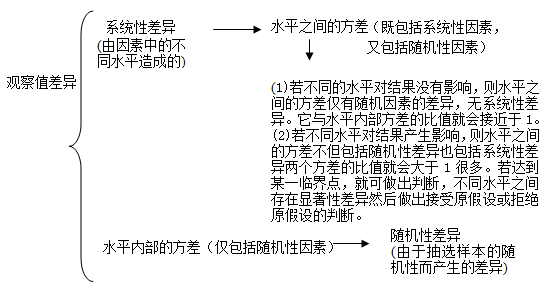
方差分析的思路是将所有样本的总变动分成两个部分，一部分是组内变动（within groups），代表本组内各样本与该组平均值的离散程度；另一部分是组间变动（between groups），代表各组平均值关于总平均值的离散程度。将这两个变动部分除以它们所对应的自由度，即得到均方差。然后，用组间变动的均方差除以组内变动的均方差，即可得到F检验值，根据统计值对应的显著性水平就可以判断不同组间是否有显著性的差异。事实上，如果不同组间的差异越大，组内的离散程度越小，那么组间变动的均方差越大，组内变动的均方差越小，即F值越大，越容易通过显著性水平检验。方差分析（Analysis of variance）能够解决多个均值是否相等的检验问题。节省时间是这种方法的明显优点。

三、F分布

水平间方差（组间方差）和水平内方差（组内方差）之比是一个统计量，数理统计证明，这个统计量服从F分布：

• 1、在方差分析中，（ ）是反映样本数据与其他组平均值的差异。【单项选择】。    
  　　 A 组间误差 
  　　 B 组内误差
  　　 C 抽样误差
  　　 D 总离差
  
  教师解析：答案B。