当前位置:课程学习>>第七章 方差分析>>学习内容>>知识点三
知识点三:双因素方差分析
○ 教师解析
一、双因素方差分析的类型

双因素方差分析有两种类型:一种是无交互作用的双因素方差分析,它假定因素A和因素B的效应之间是相互独立的,不存在相互关系;另一种是有交互作用的方差分析,它假定A、B两个因素不是独立的,而是相互起作用的,两个因素同时起作用的结果不是两个因素分别作用的简单相加,两者的结合会产生一个新的效应。这种效应的最典型的例子是,耕地深度和施肥量都会影响产量,但同时深耕和适当的施肥可能使产量成倍增加,这时,耕地深度和施肥量就存在交互作用。两个因素结合后就会产生出一个新的效应,属于有交互作用的方差分析问题。本文主要论述无交互作用的双因素方差分析。
二、数据结构
(一)双因素方差分析的假定条件
1.个总体都服从正态分布:对于因素的每一个水平,其观察值是来自正态分布总体的简单随机样本;
2.各个总体的方差必须相同:对于各组观察数据,是从具有相同方差的总体中抽取的;
3.观察值是独立的
(二)数据结构
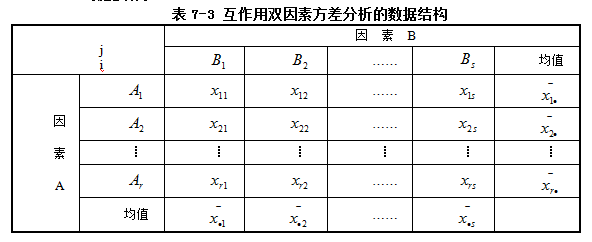
设两个因素分别是A和B。因素A共有r个水平,因素B共有s个水平,无交互作用的双因素方差分析的数据结构如表7-3所示。
(三)分析步骤
1.模型与建立假设
方差分析模型如下:
![]()
其中Xij表示第i组的第j个观察值;μ表示总体的平均水平;aj表示影响因素A在i水平下对应变量的附加效应,bj表示影响因素B在j水平下对应变量的附加效应,并满足:
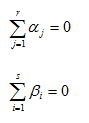
eij为一个服从正态分布的随机变量,代表随机误差。我们检验因素A是否起作用实际上就是检验各个aj是否均为0,如都为0,则因素A所对应的各组总体均数都相等,即因素A的作用不显著;对因素B,也是这样。因此原假设有两个:
对因素A:![]()
对因素B:![]()
2.构造检验F统计量
(1)水平的均值
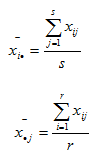
(2)总均值
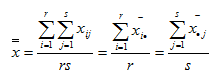
(3)离差平方和的分解
双因素方差分析同样要对总离差平方和SST进行分解,SST分解为三部分:SSA、SSB和SSE,以分别反映因素A的组间差异、因素B的组间差异和随机误差的离散状况。
它们的计算公式分别为:
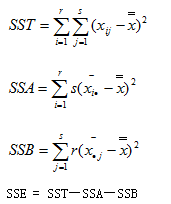
(4)构造检验统计量
由平方和与自由度可以计算出均方,从而计算出F检验值,如表7-4。
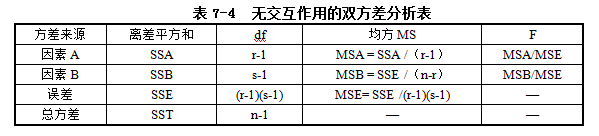

3.判断与结论
根据给定的显著性水平α在F分布表中查找相应的临界值Fa,将统计量F与Fa进行比较,作出拒绝或不能拒绝原假设H0的决策。
若A统计量大于临界值,则拒绝原假设1,表明均值之间有显著差异,即因素A对观察值有显著影响;若A统计量小于临界值,则不能拒绝原假设1,表明均值之间的差异不显著,即因素A对观察值没有显著影响;同理,若B的统计量大于临界值,则拒绝原假设2,表明均值之间有显著差异,即因素B对观察值有显著影响。 若B统计量小于临界值,则不能拒绝原假设2,表明均值之间的差异不显著,即因素B对观察值没有显著影响。
○ 边学边练
一家汽车制造商准备购进一批轮胎。考虑的因素主要有供应商和磨损程度。为例对磨损程度进行测试,分别在低速(40km/h),中速(80km/h),高速(120km/h)下进行测试,下面是从5家供应商抽取的轮胎随机样本在行驶1000km后的磨损程度。
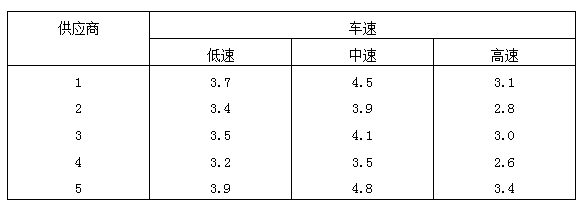
取显著性水平α=0.01,检验:
不同车速对磨损程度是否有显著性影响。
不同供应商生产的轮胎的磨损程度是否有差异。
○ 教师解析
对列因素(车速):原假设:不同车速对轮胎磨损程度没有显著影响;
备择假设:不同车速对轮胎磨损程度有显著影响;
对行因素(供应商):原假设:不同供应商对轮胎磨损程度没有显著影响;
备择假设:不同供应商对轮胎磨损程度有显著影响;
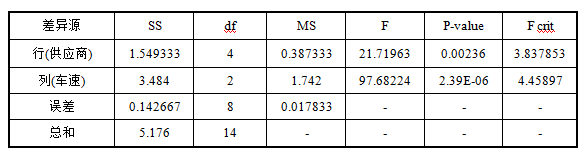
答:根据方差分析,
对于行因素,P=0.000236<0.01,所以拒绝原假设。说明不同供应商生产的轮胎对磨损程度有显著影响。
对于列因素,p=2.39E-06<0.01,所以拒绝原假设,说明不同车速对磨损程度有显著影响。
