一、方差分析的内容

（一）方差分析中的常用术语

1.因素（Factor）

因素是指所要研究的变量，它可能对因变量产生影响。一个是因素，因素是一个独立的变量，是方差分析研究的对象。要分析不同销售方式对销售量是否有影响，所以，销售量是因变量，而销售方式是可能影响销售量的因素。

2.水平（Level）

因素中的内容称为水平。水平指因素的具体表现，如销售的四种方式就是因素的不同取值等级。有时水平是人为划分的，比如质量被评定为好、中、差。

3.单元（Cell）

单元指因素水平之间的组合。如销售方式一下有五种不同的销售业绩，就是五个单元。方差分析要求的方差齐就是指的各个单元间的方差齐性。

4.元素（Element）

元素指用于测量因变量的最小单位。一个单元里可以只有一个元素，也可以有多个元素。

5.均衡（Balance）

如果一个试验设计中任一因素各水平在所有单元格中出现的次数相同，且每个单元格内的元素数相同，则称该试验是为均衡，否则，就被称为不均衡。不均衡试验中获得的数据在分析时较为复杂。

6.交互作用（Interaction）

如果一个因素的效应大小在另一个因素不同水平下明显不同，则称为两因素间存在交互作用。当存在交互作用时，单纯研究某个因素的作用是没有意义的，必须分另一个因素的不同水平研究该因素的作用大小。如果所有单元格内都至多只有一个元素，则交互作用无法测出。

若方差分析只针对一个因素进行，称为单因素方差分析。如果同时针对多个因素进行，称为多因素分析。在多因素方差分析中，双因素方差分析里最常见的。

（二）用方差分析来检验假设有三个假定

1.各个水平的观察数据必须服从正态分布：在水平Ａi下的数据是来自正态总体的一个样本，i=1,2…,r。即对于因素的每一个水平，其观察值是来自服从正态分布总体的简单随机样本，比如，每个行业被投诉的次数必需服从正态分布。

2.方差相同或者叫方差齐性：r个正态总体的方差相等，即：

各组观察数据是从具有相同方差的总体中抽取的，比如，四个行业被投诉次数的方差都相等。

3.随机性：所有数据Yij都相互独立。比如，每个行业被投诉的次数与其他行业被投诉的次数独立。

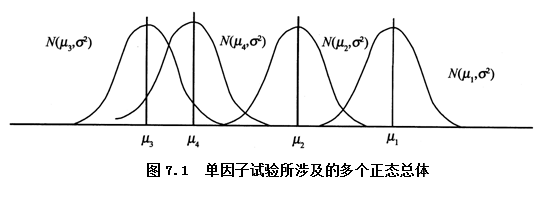
在上述假定条件下，判断行业对投诉次数是否有显著影响，实际上也就是检验具有同方差的四个正态总体的均值是否相等。如果四个总体的均值相等，可以期望四个样本的均值也会很接近，四个样本的均值越接近，推断四个总体均值相等的证据也就越充分，样本均值越不同，推断总体均值不同的证据就越充。

二、方差分析的原理

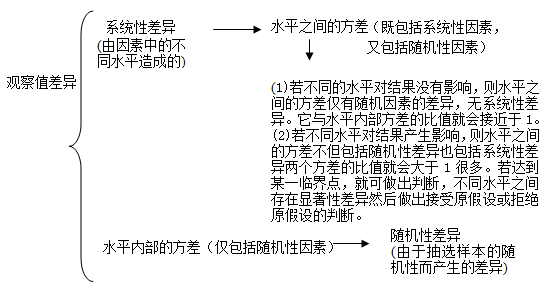
大家知道，方差分析的目的是要检验各个水平的均值μ1，μ2……μr 是否相等，实现这个目的的手段是通过方差的比较。

如果n个总体的均值相等，我们当然希望三个样本的均值比较接近，事实上，n个样本的均值愈接近，我们就愈有证据得出结论：总体均值相等，反之，若n个样本均值的差异愈大，我们就得出结论，总体均值不相等。

样本均值变动性小→支持H0，样本均值变动性大→支持H1。

三、F分布

水平间方差（组间方差）和水平内方差（组内方差）之比是一个统计量，数理统计证明，这个统计量服从F分布：