一、建立假设

方差分析的第一步是建立假设。以饮料颜色对销售量的影响为例，针对我们关心的问题提出原假设和备择假设。

H0：μ1=μ2=μ3=μ4    颜色对销售量没有影响

H1：μ1，μ2，μ3，μ4 不全相等，颜色对销售量有影响。

注意：拒绝原假设，只表明至少有两个总体的均值不相等，并不意味着所有的均值都不相等。

二、计算水平均值

三、计算离差平方和

在单因素方差分析中，离差平方和有三个，它们分别是总离差平方和，误差项离差平方和以及水平项离差平方和。

（一）总离差平方和。用SST（Sum of Squares for Total）代表，即

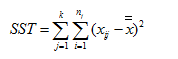
（二）误差项离差平方和（组内），用SSE（Sum of Squares For Error）代表，有时也用Within来表示组间即SSW，以SSE为例其计算公式为：.

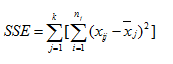
SEE或SSW反映的是水平内部，或组内观察值的离散状况，实质上反映了随机因素带来的影响。

（三）水平项离差平方和（组间）

若把单因素方差分析中的因素称为A或b，则水平项离差平方可以用SSA（Sum of Squares for factor A）或中间（bossom）即SSb表示。以SSA为例的计算公式为：

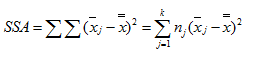
说明：用各组均值减去总均值的离差的平方，乘以各组观察值个数nj，然后加总，即可得到SSA，它的表现的是组间差异，其中即包括随机因素，也包括系统因素。

SST，SSE，SSA之间的关系：SST=SSE+SSA

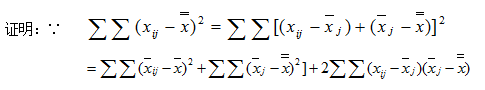
在各组同为正态分布，等方差条件下，等式右边 最后一项为零。则有：

SST=SSE+SSA

四、计算平均平方

用离差平方和除以自由度即可得到平均平方。对SST来说，其自由度为n-1。对SSA来说，其自由度为r-1，这里r表示水平的个数。对SSE来说，其自由度为n-r。SST、SSA、SSE之间的自由度也存在着如下的关系：

n-r=(r-1)+(n-r)

所以：对于SSA或SSb，其平均平方MSA或MSb为：

对于SSE，其平均平方MSE或MSW为：

五、方差分析表

F值的计算为：

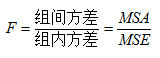
把前面一系列有关计算结果列成表格的形式，称为方差分析表。

六、统计决策

把F值与Fa值比较：

若F＞Fa拒绝原假设，则接受备择假设。

若F＜Fa接受原假设。

七、应用实例

【例7.1】调查四个行业某一时期的利润情况，结果如下图所示。按图统计结果，计算四个行业的平均利润是否有差异。

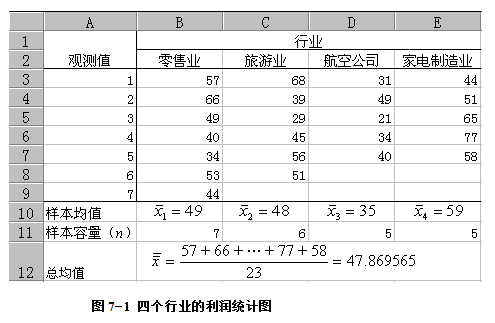
【解】

【例7.2】从某学校同一年级中随机抽取19名学生，再将他们随机分成4组，在2周内4组学生都用120分钟复习同一组英语单词。

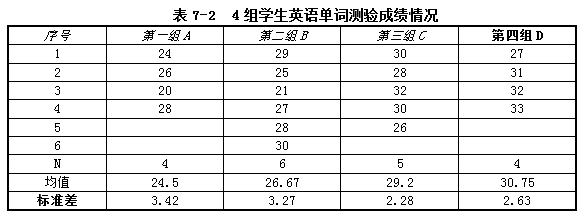
第一组每个星期一一次复习60分钟；第二组每个星期一和三两次各复习30分钟；第三组每个星期二、四、六三次复习各20分钟；第四组每天（星期天除外）复习10分钟。2周复习之后，相隔2个月再进行统一测验，其结果如下表所示。运用方差分析法可以推断分析的问题是：这4种复习方法的效果之间有没有显著性差异？

【解】

1.确定类型：由于19名学生是以随机方式被分配到四个实验组的，所以这四组样本是四个独立样本。

2.用方差分析方法对四组总体平均数差异进行综合性地F检验

检验步骤如下：

用上述公式来计算F检验统计量的值。由第四章第三节中加权平均数的计算公式得到：