一、相关表

将现象之间的相关关系，用表格来反映，这种表称为相关表。相关表的编制，一般以x为自变量，y为因变量，每个自变量都有它想对应的因变量，在表格中一一对应的排列。通过相关表可以初步看出相关关系的形式、密切程度和相关方向。相关表主要有以下几种。

1.简单相关表。按两列成对的变量数值编制的统计表，称为简单相关表。例如，某地工业局所属10个同类型企业，1993年生产性固定资产价值与工业总产值具有相关关系，编制相关表8-1。

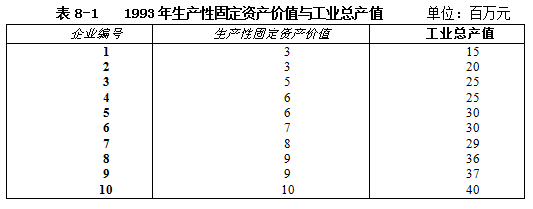
从上表可以粗略看出，随着生产性固定资产增多，工业总产值有增加的趋势。

2.分组相关表。如果原始资料很多，运用简单相关表来表示，就很难使用了。这时就要将原始资料进行分组，然后编制相关表，这种相关表称为分组相关表。分组相关表包括单变量分组表和双变量分组表两种。

(1)单变量分组表。在原始资料比较多时，对自变量数值进行分组，计算出各组的次数和因变量组平均数的统计表，称为单变量分组表。例如，根据某纺织厂1993年每个工人看管织机台数和布匹的时劳动生产率的资料，编制单变量分组相关表如表8-3。

表8-3是只将工人按看管织机台数分组，而未按时劳动生产率分组的单变量分组表。从表中可以粗略的看出，随着各组工人看管织机台数的增加，时劳动生产率有提高的趋势。

(2)双变量分组表。对两种有关变量都进行分组，交叉排列，并列出两种变量各组间的共同次数，这种统计表称为双变量分组表。列如，根据某省建材局的运材队1993年汽车运材成本和运量的资料，编制双变量分组表8-4。

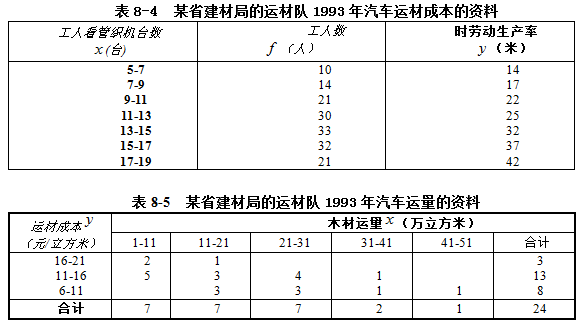
制作双变量分组相关表，须注意将自变量防在横栏，按变量值从小到大自左至右排列，将因变量放在纵栏，按变量值从大到小自上而下排列。这样做的目的是将相关表与相关图一致起来，便于判断相关关系的性质。

通过双变量相关表中各组次数分布的情况，可初步判断两种变量间相关的形态、方向和程度。例如衬衫的生产，必须考虑各种体型的消费者所需要的规格型号。为了适销对路，服装厂就需要进行抽样调查，将领口、袖长按不同的规格进行交叉分组，编制相关表，计算它们在各组的共同次数占总次数的比例，以决定生产各种不同规格衬衫的数量。有关类似问题，都可以使用相关表。

3.相关图。将现象之间的关系，通过图象来表示，这种图象称为相关图。在坐标图上，以横轴表示自变量，纵轴表示因变量，标出每对变量值的总表点(散步点)，表示其分布状况的图形即为相关图。相关图又称为散点图、散布图。通过相关图，可以大致看出两个变量之间有无相关关系，及相关的形态、方向和密切程度，其判断方法如下：

（1）强正相关。当变量x的数值增大时，变量y的数值也明显增大，相关点的分布集中呈直线形状，说明这两个变量间是强正相关。如图8-3。

（2）弱正相关。当变量x的值增大时，变量y的值也增大，但其相关点的分布比较分散，这表明两个变量间是弱相关。如图8-4。

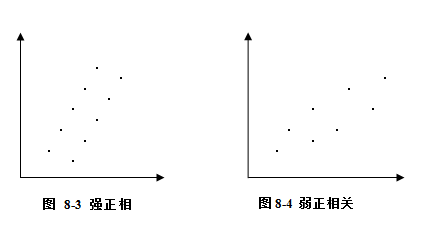
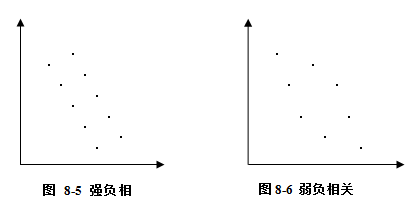
（3）强负相关。若变量x的数值增大时，变量y的数值显著减少，相关点的分布集中呈直线状，反映了两个变量间的强负相关。如图8-5。

（4）弱负相关。若变量x的数值增大时，变量y的数值趋于下降，但相关点的分布较松散，这是两个变量间弱负相关的图像。如图8-6。

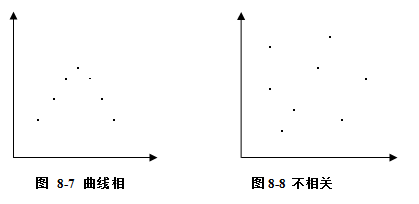
（5）非线性相关(曲线相关)。当变量x的数值增大时，各相关点的分布呈曲线状，这是非线性相关的表示。如图8-7。

（6）不相关。在图象上各相关点很分散，它说明变量x和变量y没有相关关系。如图8-8

二、相关系数

(一)相关系数的计算

相关系数是在线性相关条件下用来说明两个变量之间相关关系密切程度的统计分析指标。相关系数的定义公式为：

由于它是通过将各个离差相乘的方法来说明相关程度的，所以通常把这种相关系数的公式叫做“积差法”相关系数公式。

上式是根据，的数值计算的，当、为除不尽的小数时，计算即麻烦又影响其准确性。在实际问题中，如果根据原始变量的数值计算相关系数，可运用相关系数简捷法计算：

此式可以不用计算两个变量数列的平均值与标准差，节约工作量，而且可以减少计算平均值除不尽所带来的误差。

一般情况下，相关系数的绝对值介于0-1之间。在0.3以下者表明关系微弱，0.3-0.5者表明存在低度相关，0.5-0.8者表明显著相关，0.8以上者为高度相关。

(二)相关系数的一些重要性质

1.相关系数的取值范围，是在-1和+1之间，

即| r |≤1  或-1≤r≤+1

2.r＞0为正相关  r＜0为负相关

3.r= +1 表示x与y之间完全正相关，所有的对应点都在一条直线上。

r= -1 表示x与y之间完全负相关，对应点也都在一条直线上。

上述两种情况实际上是一种线性函数关系，不含统计学中研究的主要内容。

4.r=0时，说明x与y之间无线性相关关系

并不能说明x与y无任何关系。统计学主要研究线性相关关系。

5.| r |的数值愈大，愈接近于1，表示x与y直线相关程度愈高；反之| r |的数值愈小，愈接近于0。表示x与y直线相关程度愈低。通常判断的标准是：

| r |≤0.3 称为微弱相关

0.3＜| r |≤0.5 称为低度相关

0.5＜| r |≤0.8 称为显著相关

0.8＜| r |≤1  称为高度相关

(三)相关系数的特点

1.两个变量是对等的关系

在相关分析中，不必确定两变量中哪个是自变量，哪个是因变量，改变两变量的地位并不影响相关系数的数值。

2.只能计算出一个相关系数

3.相关系数有正负号

4.相关的两个变量必须都是随机的。在相关分析中，两变量都是随机变量。