本章练习一答案

---

一、单项选择

1.A 2.A 3.D

二、解答题

（1）解：首先，建立原假设和对立假设：H0：和H1：，然后计算检验统计量的值

若选定显著性水平0.05，根据自由度n-2=8，查分布表，得临界值2.306。

因为计算出的t值为16.0357大于临界值，因此拒绝原假设H0，接受对立假设H1。表明样本相关系数在统计上是显著的，可以作为总体相关系数的代表值，即业务考试成绩与每月销售额之间存在着高度正相关关系。

（2）解：

回归系数的显著性检验（t检验）

假设业务考试成绩对每月销售额的影响不显著，二者之间不存在线性关系，即

H0：，H1：。

计算检验统计量的值

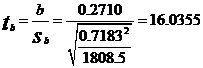
确定显著性水平0.05，根据自由度df=n-2=8，查t分布表得：

 

拒绝，接受。

说明业务考试成绩对每月销售额的影响是显著的，二者之间确实存在着线性关系。

回归方程的显著性检验（F检验）

建立假设  H0：回归方程不显著

H1：回归方程显著

计算检验统计量的值

确定显著性水平0.05，根据自由度df1=1，df2=n-2=8，查F分布表得临界值

  F=257.412>F0.05(1,8)

  拒绝，接受。

说明回归方程是显著的。职工每月销售额受业务考试成绩的显著影响。

需要说明的是：在一元线性回归分析中，只有一个自变量，t检验和 F检验是等价的。即：如果原假设被t检验拒绝或接受，也同样会被F检验拒绝或接受。但是在多元线性回归分析中，t检验和F检验是不同的，t检验是检验回归方程中各回归系数的显著性，F检验是检验整个方程回归关系的显著性。

(3)解  当=90时，=-12.191+0.2710×90=12.1985，通过计算得：

=0.7183     =76.5

当1-=95%时，、

=

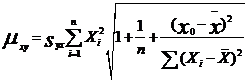
=0.7871

所以，业务考试成绩为90分，每月销售额95%的预测区间为：

即（10。3834，14.0136）。