当前位置:课程学习>>第九章 统计指数>>学习内容>>知识点二
知识点二:综合指数
○ 教师解析
一、综合指数的概念和特点
总指数的计算形式有两种,即综合指数和平均指数。本节介绍综合指数的编制方法。
综合指数是编制和计算总指数的一种基本形式,它是由两个总量指标对比而形成的指数。在所研究的总量指标中,包含两个或两个以上的因素,将其中一个或一个以上的因素指标固定下来,仅观察其中一个因素的变动,这样编制出来的总指数就叫综合指数。
综合指数从编制方法来看,具有以下特点:
(一)先综合后对比。即先解决总体中各个个体由于使用价值、经济用途、计量单位、规格、型号等不同不能直接简单相加对比的问题。为此,需要引入一个媒介因素(权数),使不能直接相加,不能直接对比的现象变成能够直接相加,能够直接对比的现象,这个因素称之为同度量因素。
(二)把总量指标中的同度量因素加以固定,以测定所要研究的因素,即指数化指标的影响程度。例如,若要观察两个时期多种商品销售总额中的销售量的影响,需要把两个时期各种商品的价格作为权数固定在同一时期,以测定两个时期各种商品销售量的影响。
(三)分子与分母所研究对象的范围原则上必须一致。
(四)综合指数的计算对资料要求较高,需要使用全面资料。
二、综合指数的编制
编制综合指数可以分别按数量指标综合指数和质量指标综合指数来进行。在编制综合指数时要注意以下两点:
(一)先要确定同度量因素。
同度量因素是指被固定的因素指标,被研究的因素指标为指数化指标,把不能直接相加的指标,过渡为可以相加计算指标的因素。
综合指数的编制方法有两个特点:
1.首先要从现象之间的联系中,确定与所要研究的现象有关联的同度量因素。
2.将引进的同度量因素固定,以测定指数化因素的变动,从而解决对比问题。
选择不同时期的数值作为同度量因素,结果不同,经济意义也不相同。
数量指标指数选用质量指标为同度量因素。一般将同度量因素的时期固定在基期。
质量指标指数选用数量指标为同度量因素,一般将同度量因素的时期固定在报告期。
(二)确定同度量因素的固定时期
拉氏指数是同度量因素固定在基期的综合指数。1864年德国学者拉斯贝尔斯(Laspeyres)提出的一种价格指数计算方法,该方法在计算一组商品价格的综合指数时,把作为权数的销售量固定在基期,计算公式为:

帕氏指数是同度量因素固定在报告期的综合指数。由另外一位德国统计学家帕煦(Paashe)于1874年提出的,故又称为帕氏指数,该方法在计算价格综合指数时,把作为权数的销售量固定在报告期,计算公式为:

【例9.1】设某粮油零售市场2004年和2005年3种商品的零售价格和销售量资料表9-1。试分别以拉氏指数方法和帕氏指数方法,计算3种商品的价格综合指数和销售量综合指数。
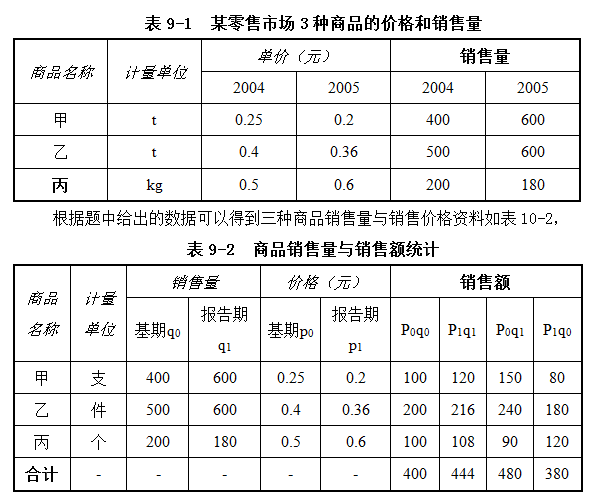
(1)根据表9-2,我们采用拉氏公式和帕氏公式计算价格综合指数:

计算结果表明 ,三种商品的价格水平平均下降5%,由于价格下跌,使商品销售额减少20元,从消费者一方看,使居民少支出20元。
 .
.
计算结果说明,三种商品的价格水平平均下降了7.5%,由于价格下跌,使商店减少销售额36元,或居民少支出36元。
(2)根据表9-2,我们采用拉氏公式和帕氏公式计算销售量综合指数:

计算结果表明,三种商品的销售量平均增长20%,由于销售量增长使商店增加销售额80元,或居民由于多购买商品而增加支出80元。

计算结果说明,三种商品的销售量平均增长16.8%,由于销售量增长而使商店增加销售额64元。
从上面的计算可以看出采用不同指数公式得到结果不同,原因是拉氏指数与帕氏指数选取的同度量因素不同,所以即使利用同样的资料来编制指数,两者的结果一般不会相同。拉氏指数以基期销售量为权数,可以消除销售量变动对价格指数的影响,从而使不同时期的指数具有可比性。但拉氏指数也存在一定的缺陷。它在假定销售量不变的情况下报告期价格的变动水平,这一指数尽管可以单纯反映价格的变动水平,但确不能反映出消费结构的变化。因此,拉氏价格指数在实际中应用较少。帕氏指数因以报告期销售量为权数,不能消除权数变动对价格指数的影响,因而不同时期的指数缺乏可比性。但帕氏指数可以同时反映出价格和消费结构的变化,具有比较明确的经济意义,因此,在实际应用中,常采用帕氏公式计算价格指数。
○ 边学边练
- 1、在销售量综合指数
 中,
中, 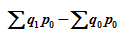 表示( )?【单项选择】
表示( )?【单项选择】
A 商品价格变动引起销售额变动的绝对额
B 价格不变的情况下,销售量变动引起销售额变动的绝对额
C 价格不变的情况下,销售量变动的绝对额
D 销售量和价格变动引起销售额变动的绝对额
