一、抽样判断

如果我们掌握了所研究的总体的全部数据，那么只需要作一些简单的统计描述就可以得到有关总体的数量特征，比如，总体的方差、均值等。但实际的情况比较复杂，有些现象的范围比较广，不可能对总体中的每一个单位都进行测定，或者有些总体的单位数较多，不可能也没必要进行一一测定。这就需要从总体中抽取一部分单位进行调查，进而利用样本提供的信息来推断总体的数量特征。例如要检验一批灯泡的使用寿命，由于测试是破坏性的，不可能对每一个灯泡都进行测试。只能抽取一部分灯泡作测试，据此来推断该批灯泡的平均使用寿命。
上述例子说明当总体的范围难以确定时，或者对于破坏性的试验，我们只能从中抽出一部分单位进行调查，依此来推断所研究总体的状况。从所研究的总体全部元素（单位）中抽取一部分元素（单位）进行调查，并根据样本数据所提供的信息来推断总体的数量特征叫样本推断。       

二、抽样方法

样本是按照一定的抽样规则从总体中抽取的一部分元素的集合。根据抽取的原则不同，抽样方法有概率抽样和非概率抽样两种。概率抽样是根据一个已知的概率来抽取样本，也就是说哪个单位被抽中与否不取决于研究人员的主观意愿，而是取决于客观的机会—概率。而非概率抽样则是研究人员有意识地选取样本单位，样本单位的抽取不是随即的。一般的抽样判断都是建立在概率抽样的基础上，因为这样的抽样方法可以用一定的概率来保证把抽样误差控制在规定的范围之内。本章所讨论的抽样推断方法都是以概率抽样为基础。

常用的概率抽样方法主要有以下几种：

（一）简单随机抽样

简单随机抽样也称纯随机抽样或完全随机抽样，是指未对总体中的个体进行事先分组或组合，直接从总体中完全随机地抽取样本的一种抽样形式。简单随机抽样是其他抽样方法的基础。简单随机抽样有两种抽取元素的方法：重复抽样和不重复抽样。

重复抽样是指从总体中抽取一个元素后，把这个元素放回到总体中再抽取第二个元素，直到抽取n个元素为止。不重复抽样。不重复抽样是从全及总体中抽取第一个样本单位，记录该单位有关标志表现后，这个样本单位不再放回全及总体中参加下一次抽选。然后，从总体N-1个单位中随机抽选第二个样本单位，记录了该单位有关标志表现以后，该单位也不再放回全及总体中去，再从全及总体N-2单位中抽选第三个样本单位，照此下去直到抽选出n个样本单位。可见，不重复抽样时，总体单位数在抽选过程中是逐渐减少的，而且各单位没有重复被抽中可能。

两种抽样方法会产生三个差别：1.抽取的样本可能数目不同；2.抽样误差的计算公式不同；3.抽样误差的大小不同。

(二)分层抽样

分层抽样也称类型抽样，是指先将总体的N个个体按某一标志分为若干层，然后每层分别抽取部分个体作为层内样本，构成总容量为n的样本，最后以样本的观测结果去估计或推断各层及总体数量特征的一种抽样组织形式。 

分层抽样的特点是必须具备总体所有个体的名录以及至少一个分层标志的全面资料，各层的抽样相互独立，样本对总体的表形取决于层内差异，与层间差异无关，要尽量把总体差异通过分层而转化为层间差异等。分层抽样适合于差异大的总体。               

等数分层抽样法是在每一层中都抽取相同单位的样本数的抽样方法。对于总体中各层的单位数基本相等或差异不大的情形，用这种方法分配样本数比较简单，否则用这种方法所产生的抽样误差就较大。

最优分配的分层抽样法是一种按照各层单位的差异大小来决定样本数的抽样方法。这种方法主要是考虑总体单位在分层以后，不仅各层所包含的单位数不同，而且各层的标志变动程度亦不同，在决定抽样单位时，对于标志变动程度大的层，抽样单位数要多，对于变动程度小的层，抽样单位数可以相应少些。这样就可以使各层所抽取的样本数在样本总数中的比例与该层的变动程度在所有变动程度总和中的比例相等。这种样本分配方式可以使样本的抽样误差最小。但是由于在决定样本数前，难以知道各层内单位的变动程度，所以这种方法实际上也很少采用。

例如：假定某大学的商学院想对今年的毕业生进行一次调查，以便了解他们的就业倾向。该学院有5个专业：会计、金融、市场营销、经营管理、信息系统。今年共有1500名毕业生，其中会计专业500名，金融专业350名，市场营销专业150名，信息系统专业200名。假定要选取180人作为样本，各专业应抽取的人数分别为：会计专业45名，金融专业40人，市场营销专业35人，营销管理专业30人，信息系统专业30人。

（三）整群抽样

整群抽样就是将总体中的单位按一定的标志或要求分成若干群，然后以群为单位，随机地抽取几个群，对已抽中的群进行全面调查或抽样调查的一种抽样方式。

采用整群抽样时，抽取的样本单位比较集中，因此，抽样调查实施起来就比较简单方便，可以节省人力、物力和财力。这种方法适宜于总体中所包括的单位数很多，而对其中单位的情况缺乏了解，直接对单位进行抽样的误差难以控制，风险较大时进行调查。这时采用整群抽样却可能获得较好的结果。

进行整群抽样时所得到结果的可靠性程度取决于，在对总体分群后，群与群之间差异的大小及抽选的单位数的多少。如果群与群之间差异小而抽选的样本群数多，则抽样的误差就小，反之，若群与群之间的差异大，而抽选的样本群数又少，抽样的误差就大。

例如，对一城市居民进行生活水平调查，如果不是从全部城市住户中直接抽选住户进行调查，而是从城市全部居民委员会中随机抽选若干居委会，对被抽中的居委会所有住户都进行调查，这就是整群抽样。该城市的每一居委会就是一群。再如，对连续生产的企业，每小时都抽选最后10分钟生产的全部产品进行调查。那么，每小时最后10分钟生产的全部产品就是一群。如果一天24小时生产的全部产品构成全及总体，则全及总体有144群，样本有24群。

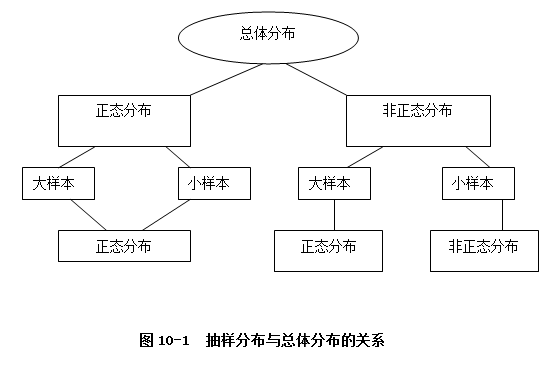
三、抽样分布

如果能把对总体中每一个单位测量的结果罗列出来就得到总体的分布。但在抽样的情形，无论对于有限总体还是无限总体，只要抽样的样本数小于总体中的单位数，那么可能抽取的样本就不只一个。在一般情况下，从同一总体中抽取出的不同样本，其统计量的值是不同的。全部可能样本的统计量的概率分布叫做抽样分布。统计上通常用样本的分布，即抽样分布来近似总体分布，例如，我们可以使用样本的均值和标准差来描述总体的均值和标准差的分布，使用样本的比例来描述总体比例的分布。

（一）样本均值的抽样分布

在理论上可以证明，若总体服从均值为m，方差为s2的正态分布，则从总体中抽取出的样本的均值仍然是服从正态分布的。下面我们研究样本均值的抽样分布特征。

假设我们从均值为m，方差为s2的总体中抽取一组样本，它们相互独立，且具有相同的分布函数。利用期望值的运算性质，我们研究样本均值的数字特征，就有：

上述结论是对正态总体而言的，不过实际上，即使对于非正态总体而言，随着样本容量的增加，的抽样分布也会近似地变成正态的。事实上，只要样本足够大（通常要求样本容量不小于45），即使是从非正态分布的总体中抽样，根据统计学中的中心极限定理，样本均值的抽样分布与从正态分布总体中的抽样所得到的结果也近似相同。

此外样本均值的方差与抽样方法有关，上述结论是针对重复抽样而言，如果在不重复抽样的条件下样本均值的方差为：

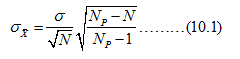
（二）样本比例的分布

管理中还需要研究总体或样本中具有某种属性的个体占全体单位数的百分比问题，由此需要研究样本的比例分布问题。总体中具有某种属性的单位数与总体全部单位数之比称为总体比例，也称总体的成数，记作P。而样本中具有某种属性的单位数与样本总数之比称为样本比例，或称样本成数，记作P。

若从总体中随机抽取出容量为n的样本，发现其中具有某种属性的单位数为m，则样本中具有某种属性的单位的比例就为

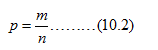
样本比例是一个随机变量，当样本容量很大时，近似地服从正态分布。其分布的数学期望为总体的成数P，方差等于P(1-P)/n，即：

但是，要使样本成数的抽样分布近似于正态分布，样本容量n必须很大，并且要满足np和n(1-p)都大于5。

简述影响抽样平均误差的若干因素

（一）总体单位之间标志值的差异程度

（二） 样本单位数目

（三） 抽样方法

（四） 抽样的组织形式