一、估计量与估计值

参数估计也就是用样本统计量去估计总体的参数。比如，用样本均值估计总体均值估计总体均值，用样本方差估计总体方差，用样本比例估计总体比例等。

如果我们将总体参数笼统地用一个符号θ来表示，参数估计也就是如何用样本统计量来估计总体参数θ。

比如，我们要估计一个班学生考试的平均分数，从中抽取一个样本，全班的平均分数是不知道的，称为参数，用θ表示，根据样本计算的平均分数就是一个估计量，用q一帽表示，假定计算出来的样本平均分数为80分，这个80分就是估计量的具体数值，称为估计值。

二、点估计与区间估计

（一）点估计

点估计又称定值估计。它是用实际样本指标数值代替总体指标数值，即总体平均数的点估计值就是样本平均数，总体成数的点估计值就是样本成数。这种估计不考虑是否有抽样误差。

例如，对一批某种型号的电子元件10000只进行耐用时间检查，随机抽取100只，测试的平均耐用时间为1055小时，合格率为91%，我们推断说10000只电子元件的平均耐用时间为1055小时，全部电子元件的合格率也是91%。

【例10.1】已知某种灯泡的寿命X~N（m，s2），其中m和s2都是已知的，今随机取得4只灯泡，测得寿命（单位：小时）为1502，1453，1367，1650，试估计m，s2。

解：因为m是全体灯泡的平均寿命, x一bar为样本的平均寿命，很自然地想到用x一ba去估计m；同理用S去估计s。

由于

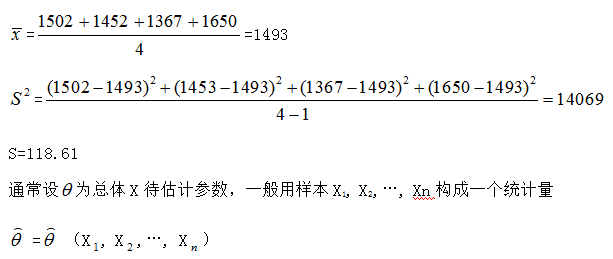
来估计q，则称q帽为q的估计量。对于样本的一组数值X1, X2,…, Xn，,估计量q帽的值q帽（X1, X2,…, Xn）称q的估计值。于是点估计即是寻求一个作为待估计参数q的估计量q帽（X1, X2,…, Xn）的问题。但必须注意，对于样本的不同数值，估计值是不相同的。如上例中，我们分别用样本平均数和样本修正方差来估计总体数学期望和总体均方差。

(二)区间估计

区间估计所表明的是一个可能范围，不是一个绝对可靠的范围。是用样本指标和它的抽样极限误差构成的区间来估计总体指标，并以一定的概率保证总体指标将在所估计的区间内。

比如，根据样本结果估计出某班级考试成绩的平均分数在75~85分之间，着就是区间估计。在实际中我们更多使用区间估计，因为我们不可能指望样本估计量的值恰好等于总体参数的值。

三、评价估计量的标准

在点估计中，我们用样本q帽作为总体参数θ的估计。实际上，用于估计θ的估计量很多，比如我们可以用样本均值作为总体均值的估计量，也可以用样本中位数作为总体均值的估计量，等等。那么，究竟用样本的哪种估计量作为总体参数的估计呢？自然是估计效果最好的那种，什么样的估计量才算是一个好的估计量呢？统计学家给出了一些标准：

(一)无偏性。即以抽样指标估计全及指标要求抽样指标值的平均数等于被估计的全及指标本身。就是说，虽然每一次的抽样指标(如x，p等)和未知的全及指标(如X，P等)可能不相同，但在多次反复的估计中各个抽样指标的平均数应等于全及指标，即抽样指标的平均来说与全及指标是没有偏误的。

(二) 一致性。即当样本容量n充分大的时，若样本指标充分地靠近被估计的全及指标，则该样本指标是被估计的全及指标的一致估计量。

(三) 有效性。即如果一个样本估计量的方差比其他估计量的方差小，则称该样本估计量是被估计的全及指标的有效估计量。对同一总体参数的两个无偏估计量θ1帽和θ2帽，若：

我们称θ1帽比θ2帽更有效，是个更好的估计。即θ1帽方差比θ2的方差小，从而θ1的值比θ2的值更接近总体参数。

简述抽样估计的优良标准

（一）无偏性：指样本指标的平均数等于被估计的总体指标。

（二）有效性：用样本指标估计总体指标时，若某样本指标的方差比其他估计量的方差小，则称该样本指标是总体指标的最有效的估计量。

（三）一致性：以样本指标估计总体指标，要求当样本单位数相当大时，样本指标充分靠近总体指标，则称这个估计量为一致的估计量。