一、单项选择

1.从服从正态分布的无限总体中分别抽取容量为4，16，36的样本，当样本容量增大时，样本均值的标准差将（   ）

A.增加   

B.减小   

C.不变    

D.无法确定

2.某班级学生的年龄是右偏的，均值为20岁，标准差为4.45.如果采用重复抽样的方法从该班抽取容量为100的样本，那么样本均值的分布为（    ）

A.均值为20，标准差为0.445的正态分布

B.均值为20，标准差为4.45的正态分布

C.均值为20，标准差为0.445的右偏分布

D.均值为20，标准差为4.45的右偏分布

3.区间估计表明的是一个 (    )

A.绝对可靠的范围   B.可能的范围  C.绝对不可靠的范围  D.不可能的范围

4.在其他条件不变的情形下，未知参数的1-α置信区间， （   ）

A.α越大长度越小        

B.α越大长度越大    

C.α越小长度越小         

D.α与长度没有关系

5.设总体服从正态分布，方差未知，在样本容量和置信度保持不变的情形下，根据不同的样本值得到总体均值的置信区间长度将 （    ）

A.增加    

B.不变  

C.减少   

D.以上都对

6．在其他条件不变的前提下，若要求误差范围缩小1／3，则样本容量 （    ）

A.增加9倍  

B.增加8倍     

C.为原来的2.25倍 

D．增加2.25倍

二、简答题

简述抽样估计的优良标准

三、计算题

1.假设2010年中国所有中型公司首席执行官每年薪水的增长百分比服从均值为12.2%，标准差为3.6%的正态分布。现在选取一个容量为9的样本，并且已经计算出了样本均值，那么样本均值小于10%的概率为多少？

2.（样本容量的大小）某型号所有汽车的耗油量均值为25英里每加仑、标准差为2.假设该总体服从正态分布，从这些汽车耗油量中抽取一个随机样本。请分别求出样本容量为1，4，16的情形下，耗油量的平均值低于24英里每加仑的概率分别是多少？

3.美国某城市一年来新房的平均售价为115000美元，总体的标准差为25000美元。从该城市销售的房子中随机抽取100个作为样本。问：

（1）售价样本均值超过110000美元的概率为多少？

（2）售价样本均值在113000~117000美元之间的概率为多少？

（3）售价样本均值在114000~116000美元之间的概率为多少？

（4）不通过计算，请指出售价的样本均值最可能落入下面的哪个区间？

1）113000~115000美元，2）114000~116000美元，3）115000~117000美元，4）116000~118000美元

（5）假设你已经计算了上述结果，而你的朋友声称该城市新房售价的总体分布基本不是正态分布，你对此如何应答？

4、设年末某储蓄所对某类储蓄存款户账号随机抽取100户的资料如下：

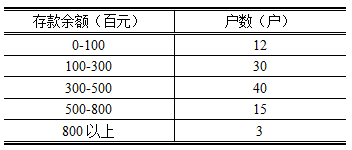
（1）根据上述材料，应用点估计方法估计这类储蓄账户的平均余额，并计算抽样平均误差；

（2）试以95%的概率，估计该储蓄所存款户平均每户的存款余额的置信区间。

5、松江A、B两所大学某学期期末高等数学考试采用同一套题目，Ａ校认为该校学生高数考试成绩比Ｂ校学生成绩高10分以上。为了验证这个说法，主管部门从A校随机抽取75人作为样本，测得其分数平均值为78.6分，标准差为8.2分；B校抽取了80个同学作为随机样本，测得分数平均值为73.8分，标准差为7.4分，试在99％的把握下确定两校平均分之差的置信区间，根据此置信区间主管部门能够得到什么结论？