当前位置:课程学习>>第二章 坐标系统>>电子教案>>知识点一
知识点一:地理坐标系统
1.1地理坐标系统
地理坐标系(Geographic Coordinate System,GCS),是使用三维球面来定义地球表面位置,以实现通过经纬度对地球表面点位引用的坐标系。也就是说,地理坐标系实际是一种球面坐标系统。
GIS的研究对象是具有空间内涵的地理数据,地理数据与其位置的识别联系在一起。要确定地面点的位置,必须确定和描绘地球的形状。地球是一个两极略扁的旋转球体,表面高低起伏,相差悬殊。其内部结构和质量分布复杂易变,人们很难用简单的数学方程来准确地描述真实地球的形状,只能用近似的方法来表示,依靠测量方法和精度的不断改进、理论研究的不断深入而逐步逼进真实的地球。由于地球是一个质体,其周围存在一个引力场,顾及地球自转,称为重力场。重力相等的点构成重力等位面。大地水准面是一个重力等位面。未受外界扰动的平均海水面是大地水准面的一部分,即通过平均海水面的重力等位面即大地水准面。大地水准面包围球体称之为大地球体。
大地水准面仍然是一个很复杂的曲面,要用一个无穷多项的函数级数才能严密的表示它。为测量和计算工作的方便,将地球抽象为形状接近于一个扁率很小的椭圆绕其短轴旋转而成的椭球体;这个绕大地球体短轴旋转所构成的旋转椭圆球体称之为地球椭球体(图2-1),并用作测量计算的基准面。
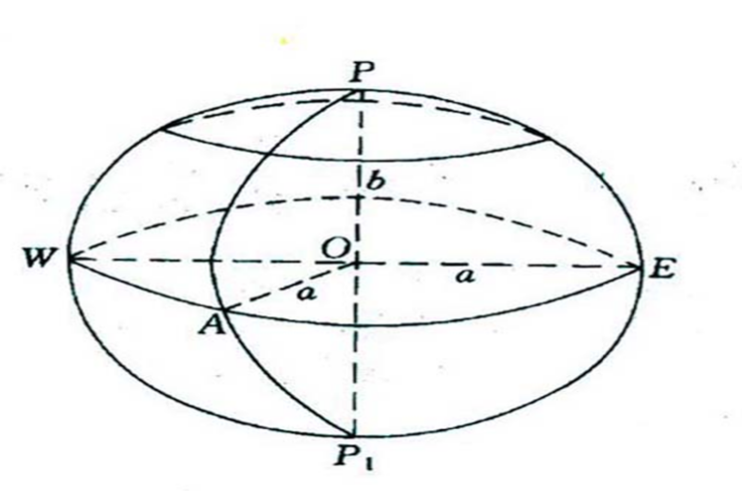
图2-1 地球椭球体
地球椭球体的表面是一个规则的数学曲面,它的大小以长半径a、短半径b和扁率σ=(a-b)/a表示。第一偏心率为e=\sqrt{\frac{a^{2}-b^{2}}{a^{2}}} ![]() ,第二偏心率为
,第二偏心率为![]() 。表2-1列举了较常见的几个椭球体数据。
。表2-1列举了较常见的几个椭球体数据。
地球形状确定之后,还需大地水准面和椭球体面的相对关系,也就是参考椭球体定位。参考椭球体,是和局部地区的大地水准面复合最好的一个地球椭球体。我国原来所采用的参考椭球有:新中国成立前的海福特椭球和新中国成立初期的克拉索夫斯基椭球。但由于克拉索夫斯基椭球参数同1975年国际第三推荐值GRS(1975)椭球体(IUGG/IAG)相比,其长半轴相差105m,因而1980年我国采用该参考椭球,建立了1980西安大地坐标系,并将大地原点设于陕西省泾阳县永乐镇。
在确定参考大地基准之后,那么地面上任意一点的位置都可以由经纬度来决定,记作( L ,B )。地面上任一点的经度为过该点的子午面和起始子午面之间所夹的二面角,纬度为过该点的法线与赤道面的交角。这样就建立了一个二维椭球面坐标系统,即地理坐标系统。
| 椭球名称 | 年代 | 长半轴a/m | 扁率α | 附注 |
| 德兰布尔 | 1800 | 6 375 653 | 1:334.0 | 法国 |
| 白塞尔 | 1841 | 6377397.155 | 1:299.1528128 | 德国 |
| 克拉克 | 1880 | 6 378 249 | 1:293.459 | 英国 |
| 海福特 | 1909 | 6 378 388 | 1:297.0 | 美国 |
| GRS(1975)椭球体(IUGG/IAG) | 1975 | 6 378 140 | 1:298.257 | 西安80坐标系参考椭球 |
| WGS-84椭球体 | 1984 | 6 378 137 | 1:298.257223 | 世界大地坐标系统G873参考椭球 |
| 2000国家大地坐标系椭球 | 2008 | 6378137 | 1:298.257222101 | CGCS2000 坐标系统参考椭球 |
