当前位置:课程学习>>第二章 坐标系统>>电子教案>>知识点二
知识点二:地图投影
2.1 投影与投影变形
由于地球是一个赤道略宽两极略扁的不规则的梨形球体,其表面是一个不可展平的曲面,故从椭球面到平面必须经过数学变换,这个数学变换称为地图投影(图2-2)。在数学中,投影指建立两个点集间一一对应的映射关系。在地图学中,地图投影指建立地球表面上的点与投影表面上点之间的一一对应关系。地图投影的基本问题就是利用一定的数学法则把地球表面上的经纬线网表示到平面上。凡是地理信息系统就必然要考虑地图投影,地图投影的使用保证了空间信息在地域上的联系和完整性。
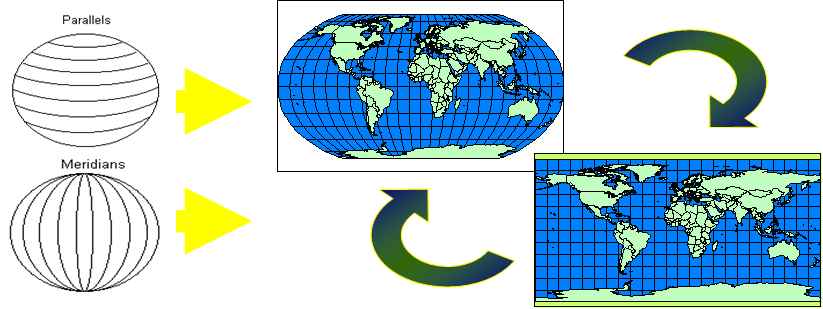
图2-2 地图投影过程
投影过程将产生投影变形,不同的投影方法具有不同性质和大小的投影变形。由于球面上任何一点的位置是用地理坐标(λ,φ)表示的,而平面上的点的位置是用直角坐标(x,у)或极坐标(ρ ,θ)表示的,所以要想将地球表面上的点转移到平面上,必须采用一定的方法来确定地理坐标与平面直角坐标或极坐标之间的关系。这种在球面和平面之间建立点与点之间函数关系的数学方法,就是地图投影方法。地图投影变形是球面转化成平面的必然结果,没有变形的投影是不存在的。
由于投影的变形,地图上所表示的地物,如大陆、岛屿、海洋等的几何特性(长度、面积、角度、形状)也随之发生变形。每一幅地图都有不同程度的变形;在同一幅图上,不同地区的变形情况也不相同。地图上表示的范围越大,离投影标准经纬线或投影中心的距离越长,地图反映的变形也越大。因此,大范围的小比例尺地图只能供了解地表现象的分布概况使用,而不能用于精确的量测和计算。地图投影的实质就是将地球椭球面上的地理坐标转化为平面直角坐标,用某种投影条件将球面上的地理坐标点一一投影到平面坐标系内,以构成某种地图投影。
2.2 地图投影分类
地图投影的种类很多,为了学习和研究的方便,应对其进行分类。由于分类的标志不同,分类方法就不同。从使用地图的角度出发,需要了解下述几种分类。
一、按变形性质分类
按变形性质,地图投影可分为等角投影、等(面)积投影、任意投影。
等角投影:投影面上某点的任意两方向线夹角与椭球面上相应两线段夹角相等,即角度变形为零。等角投影在一点上任意方向的长度比都相等,但在不同地点长度比是不同的,即不同地点上的变形椭圆大小不同。
等积投影:在投影平面上任意一块面积与椭球面上相应的面积相等,即面积变形等于零。
任意投影:多用于要求面积变形不大、角度变形也不大的地图,如一般参考用图和教学地图。其中等距投影是任意投影中比较常见的一种,其特点是沿某一特定方向的距离,投影前后保持不变。在任意投影上,长度、面积和角度都有变形,它既不等角又不等积。等距投影的面积变形小于等角投影,角度变形小于等积投影。
我们常用变形椭圆来描述投影变形特征,地面上一个微分圆投影后变成一个椭圆,即称为变形椭圆。变形椭圆的形状和大小能反映投影中变形的质和量的差别,图2-3显示了微分圆的不同变形,1,2为等角投影,3,4为等积投影,5,6为任意投影,其中5为等距投影。
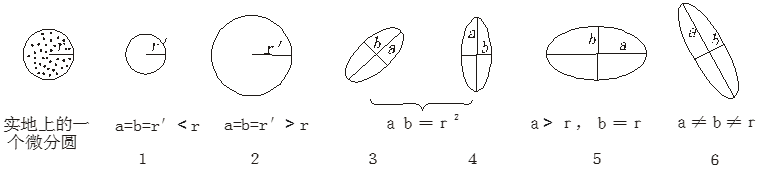
图2-3 通过变形椭圆形状显示变形特征
经过投影后地图上所产生的长度变形、面积变形和角度变形,是相互联系相互影响的。它们之间的关系是:在等积投影上不能保持等角特性,在等角投影上不能保持等积特性;在任意投影上不能保持等角和等积的特性;等积投影的形状变形比较大,等角投影的面积变形比较大。
二、按构成方法分类
根据不同的构成方法,地图投影可以分为两大类:几何投影和非几何投影。
(1)几何投影。几何投影是把椭球面上的经纬线网投影到几何面上,再将几何面展为平面而获得。根据几何面的形状,又进一步分为方位投影、圆柱投影、圆锥投影,分别包含正轴、斜轴和横轴方向上的投影(图2-4)。其中正轴投影后的经纬网形状如图2-5所示。
方位投影:以平面作为投影面,使平面与球面相切或相割,将球面上的经纬线投影到平面上而成。
圆柱投影:以圆柱面作为投影面,使圆柱面与球面相切或相割,将球面上的经纬线投影到圆柱面上,然后将圆柱面展为平面而成。
圆锥投影:以圆锥面作为投影面,使圆锥面与球面相切或相割,将球面上的经纬线投影到圆锥面上,然后将圆锥面展为平面而成。
