当前位置:课程学习>>第三章 矢量数据模型>>电子教案>>知识点二
知识点二:拓扑的概念、拓扑元素、基本拓扑关系及其表示
2.1 拓扑
“拓扑”(Topology)一词来源于希腊文,它的原意是“形状的研究”。拓扑学是几何学的一个分支,它研究在拓扑变换下能够保持不变的几何数据,即拓扑属性。拓扑性质是指在双向连续且一一对应的变换下图形不变的性质,这种变换成为拓扑变换。二维上,这种拓扑变换可用理想橡皮板拉伸、压缩来实现,故拓扑性质也可称橡皮板上空间特性。拓扑关系则是两个以上拓扑元素间的拓扑性质。 建立拓扑关系是一种对空间结构关系进行明确定义的数学方法。具有某些拓扑关系的矢量数据结构就是拓扑数据结构,拓扑数据结构是GIS的分析和应用功能所必需的,其表示方式没有固定的格式,也还没有形成标准,但基本原理是相同的。
一、拓扑元素
对二维而言,矢量数据可抽象为点(结点)、线(链、弧段、边)、面(多边形) 三种要素,即称为拓扑元素。对三维而言,则要加上体。
点(结点)——孤立点、线的端点,面的首尾点,链的连接点等。
线(链、弧段、边)——两结点间的有序弧段。
面(多边形)——若干条链构成的闭合多边形。
二、基本的拓扑关系
最基本的拓扑关系是关联和邻接。
关联——不同拓扑元素之间的关系。如结点与链,链与多边形等。
邻接——相同拓扑元素之间的关系。如结点与结点,链与链,面与面等。邻接关系是借助于不同类型的拓扑元素描述的,如面通过链而邻接。
在GIS的分析和应用功能中,还可能用到其他拓扑关系,如:
包含关系——面与其他拓扑元素之间的关系。如果点、线、面在该面内,则称被该面包含。如某省包含的湖泊、河流等。
连通关系——拓扑元素之间的通达关系。如点连通度,面连通度的各种性质及相互关系。
层次关系——相同拓扑元素之间的等级关系。如国家由省(自治区、直辖市)组成,省(自治区、直辖市)由县组成等。
拓扑元素量、质不变及相互关系——点、线、面拓扑元素质、量不变以及纯多边形地图上,有著名的欧拉公式:L + 2 = A + P
其中,P、L、A表示图上点数、线数及面数(包括无穷远面),2为欧拉示性数。这也是一种重要的拓扑关系,在拓扑一致性检验中经常使用。
实际上按前述拓扑性质定义,拓扑关系型式、数量对具体图形而言多种多样,有些也十分复杂,GIS中所用拓扑性质、拓扑关系也是多种多样的,应具体明确,泛指往往并不科学。
三、拓扑关系的表示
拓扑数据结构的关键是拓扑关系的表示,而几何数据的表示可参照矢量数据的简单数据结构。在目前的GIS中,主要表示基本的拓扑关系,而且表示方法不尽相同。
面-链关系:
| 面 | 构成面的链 |
链-结点关系:
| 链 | 链两端点的结点 |
结点-链关系:
| 结点 | 通过该结点的链 |
链-面关系:
| 链 | 左面 | 右面 |
下面举一个表示矢量数据拓扑关系的例子(图3-2).
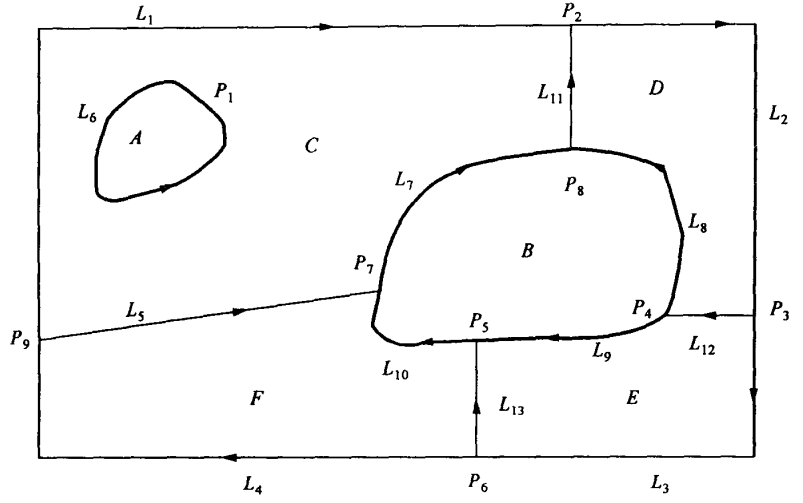
图3-2 拓扑关系示例
