当前位置:课程学习>>第四章 栅格数据模型>>学习内容>>知识点七
知识点七:矢量数据和栅格数据的转化
○ 教师讲解
我们通过上述视频简单介绍两种数据的转化方法。现在我们来进行归纳总结:
矢量—栅格转换
一、 线的栅格化方法
设直线段的两端点坐标转换到栅格数据的坐标系后为(xA,yA)、(xB,yB),则栅格化的两种常用方法为DDA法(数字微分分析法)和Bresenham法。
(1)DDA法
如图4-15所示,设(xA,yA)、(xB,yB)与栅格网的交点为(xi,yi),则
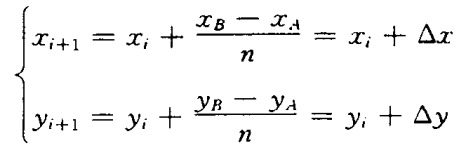
其中,
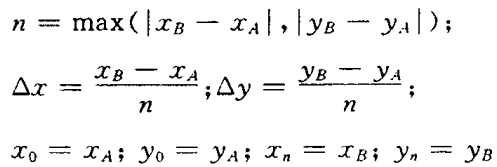
这样从i=0计算到i=n-1,即可得直线与格网的n个交点坐标,对其取整就是该点的栅格数据了。该方法的基本依据是直线的微分方程,即dy/dx=常数。其本质是用数值方法解微分方程,通过同时对x和y各增加一个小增量来计算下一步的x,y值,即这是一种增量算法。
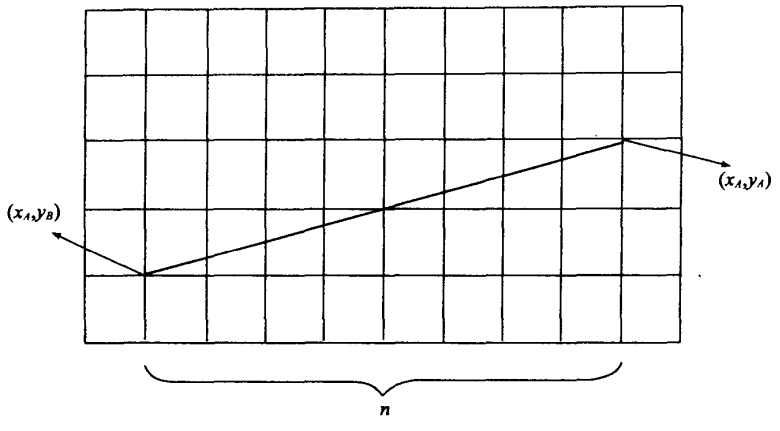
图4-15 线段变栅格示意
(2)Bresenham算法
根据直线的斜率,把直线分为8个挂限(图4-16)。例如斜率在第一挂限,范围为0.5~1,则下一点取(1,1);若斜率取0~0.5,则下一点取(1,0)。Bresenham算法不仅速度快、效果好,而且可以理论上证明它是目前同类的各种算法中最优的。
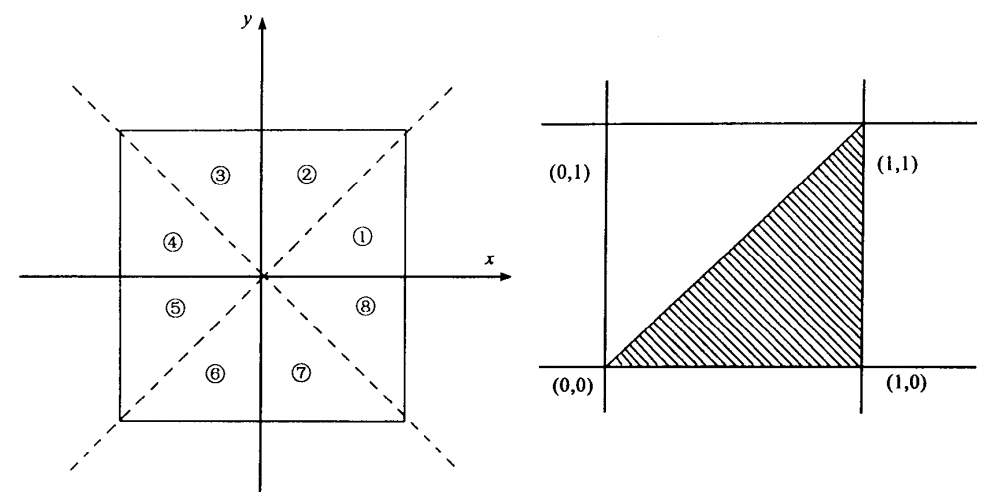
图4-16 Bresenham算法分区示意
二、 面(多边形)的栅格化方法
(1)内部点扩散法
由一个内部的种子点,向其4个方向的邻点扩散,判断新加入的点是否在多边形边界上。如果是,不作为种子点;否则当做新的种子点。直到区域填满,无种子点为止。
(2)扫描法
如图4-18,按扫描线的顺序,计算多边形与扫描线的相交区间,再用相应的属性值填充这些区间,即完成了多边形的栅格化。这种算法的缺点是计算量较大。
(3)边填充算法
其基本思想是:对于每一条扫描线和每条多边形边上的交点,将该扫描线上交点右方的所有像素取原属性值之补。对多边形的每条边作此处理,多边形的方向任意。本算法的优点是算法简单,缺点是对于复杂图形,每一像素可能被访问多次,增加了运算量。
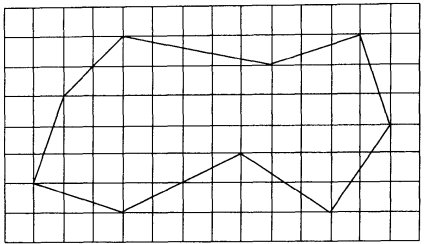
图4-18 扫描法填充示意
栅格—矢量转换
大致过程如下:
一、 二值化 由于扫描后的图像是以不同灰度级存储的,为了进行栅格数据矢量化的转换,需压缩为两级(0和1),这就称为二值化。二值化的关键是在灰度级的最大值和最小值之间选取一个阈值,当灰度级小于阈值时取值为0,当灰度级大于阈值时取值1。
二、二值图像的预处理
对于扫描输入的图幅,由于原稿不干净等原因。总是会出现一些飞白、污点、线划边缘凹凸不平等现象。对此,除了依靠图像编辑功能进行人机交互处理外,还可以通过一些算法来进行处理。
三、细化
所谓细化就是将二值图像像元阵列逐步剥除轮廓边缘的点,使之成为线划宽度只有一个像元的骨架图形。细化后的图形骨架既保留了原图形的绝大部分特征,又便于下一步的跟踪处理。细化的基本过程是:(1)确定需细化的像元集合;(2)移去不是骨架的像元;(3)重复(1)(2),直到仅剩骨架像元。
四、追踪
细化后的二值图像形成了骨架图,追踪就是把骨架转换为矢量图形的坐标序列。其基本步骤为:(1)从左向右,从上向下搜索线划起始点,并记下坐标。(2)朝该点的8个方向追踪点,若没有,则本条线的追踪结束,将(1)进行下条线的追踪;否则记下坐标。(3)把搜索点移到新取的点上,转(2)。需注意的是,已追踪点应作标记,防止重复追踪。
五、拓扑化
为了进行拓扑化,需找出线的端点和结点,以及孤立点。
孤立点:八邻域中没有为1的像元。如图4-23中(1)。
端点:八邻域中只有一个为1的像元。如图4-23中(2)。
结点:八邻域中有三个或三个以上为1的像元。如图4-23中(3)。
在追踪时加上这些信息后,就可形成结点和弧段,然后可用矢量数据的自动拓扑方法进行拓扑化。
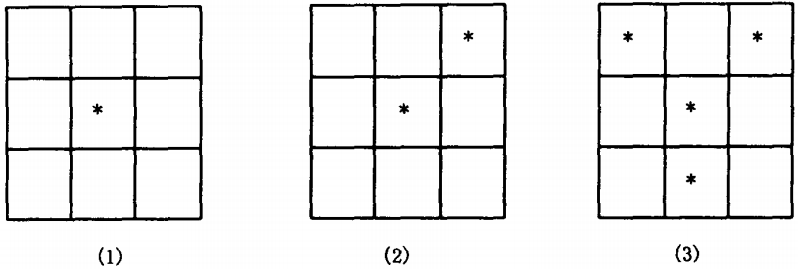
图4-23 点的拓扑性判断
矢量栅格一体化数据结构(大致了解即可,不做具体要求):参考电子教材
