当前位置:课程学习>>第四章 栅格数据模型>>电子教案>>知识点六
知识点六:栅格数据的压缩和编码
游程长度编码的优缺点如下:
优点:对于线状和较大区域具有较高的压缩率;数据检索和运算比较简单,容易完成检索、叠加、合并等操作;数据精度增加,数据量不会显著增加,对编码形式影响不大;适用于小型计算机,同时减少了栅格数据库的数据输入量。
缺点:对于图斑破碎,属性和边界多变的数据压缩效率较低,甚至压缩后的数据量比原始数据还大。计算时的处理和制图输入工作量有所增加。
三、四叉树编码(Quad tree Encoding)
四叉树是一种可变分辨率的非均匀网格系统。其基本思想是:将一幅栅格数据层或图像等分为四部分,逐块检查其格网属性值(或灰度);如果某个子区的所有格网值都具有相同的值,则这个子区就不再继续分割,否则还要把这个子区再分割成四个子区。这样依次地分割,直到每个子块都只含有相同的属性值或灰度为止。
采用四叉树编码时,为了保证四叉树分解能不断地进行下去,要求图像必须为2n×2n的栅格阵列,对于非标准尺寸的图像需首先通过增加背景的方法将图像扩充为2n ×2 n的图像。
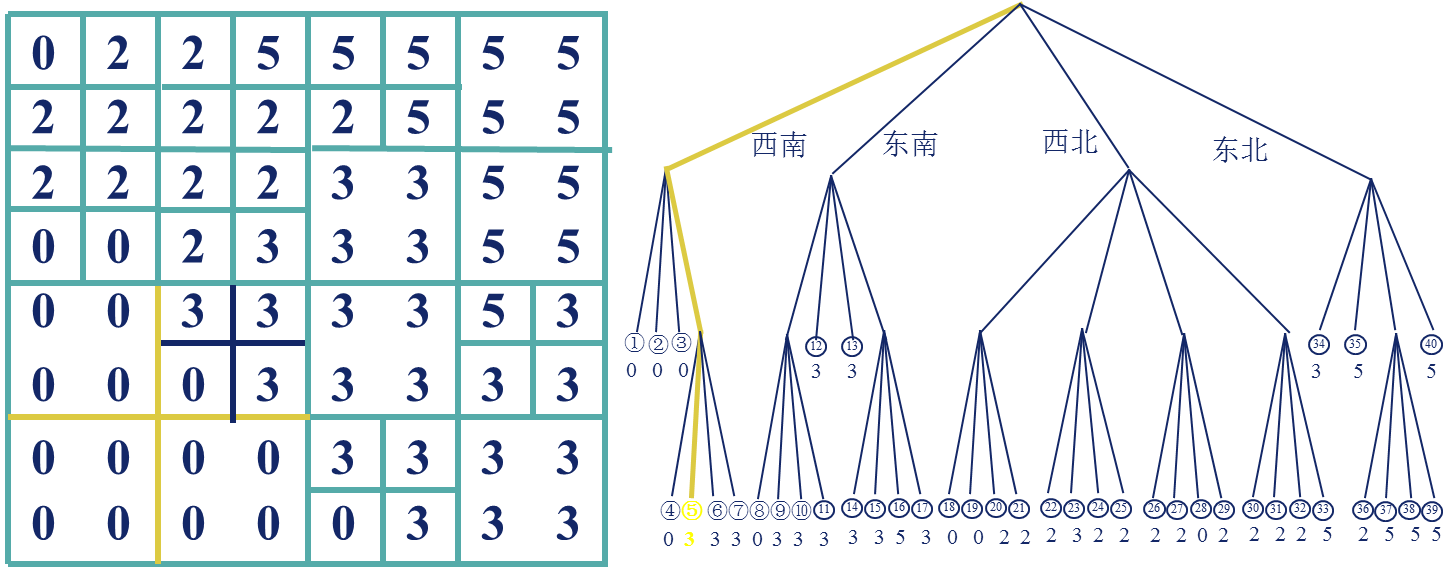
图4-14 四叉树编码示意图
四叉树结构按其编码的方法不同分为常规四叉树和线性四叉树:
常规四叉树:除了记录叶结/节点之外,还要记录中间结点(非叶结/节点)。结点之间借助指针联系,每个结点需要用六个量表达:四个叶结点指针,一个父结点指针和一个结点的属性或灰度值。这些指针不仅增加了数据贮存量,而且增加了操作的复杂性。常规四叉树主要在数据索引和图幅索引等方面应用。
线性四叉树:只存贮最后叶结点的信息。包括叶结点的位置、深度和本结点的属性或灰度值。所谓深度是指处于四叉树的第几层上。由深度可推知子区的大小。线性四叉树叶结点的编号需要遵循一定的规则,这种编号称为地址码,它隐含了叶结点的位置和深度信息。最常用的地址码是四进制或十进制的Morton码。
四叉树编码优缺点:
优点:四叉树编码具有可变的分辨率,树的深度随数据的破碎程度而变化;有区域性质,压缩数据灵活,许多数据和转换运算可以在编码数据上直接实现,大大地提高了运算效率;支持拓扑“洞”(嵌套多边形)的表达,是优秀的栅格压缩编码之一 。
缺点:其最大不足是其不稳定性,即同样的原始数据应用不同的算法进行编码可能会得到不同的编码结果,不利于数据分析。
四.其他编码
还有很多编码方法,如傅立叶变换、小波变换、余弦变换等,常常用于遥感原始数据的压缩。由于它们多数是有损压缩,一般不用于需要进行分析的栅格数据。在四叉树基础上发展而来的八叉树目前也是研究热点之一。
