当前位置:课程学习>>第四章 栅格数据模型>>电子教案>>知识点七
知识点七:栅格数据的压缩和编码
三、矢栅一体化数据结构的设计
线性四叉树编码、三个约定和多级格网法为建立矢栅一体化的数据结构奠定了基础。 线性四叉树是基本数据格式,三个约定设计点、线、面数据结构的基本依据,细分格网法保证足够精度。
(1)点状地物和结点的数据结构
根据对点状地物的基本约定,点仅有位置、没有形状和面积,不必将点状地物作为一个覆盖层分解为四叉树,只要将点的坐标转化为地址码M1和M2而不管整个构形是否为四叉树。这种结构简单灵活,便于点的插入和删除,还能处理一个栅格内包含多个点状目标的情况。
所有的点状地物以及弧段之间的结点数据用一个文件表示,其结构见表4-2。可见, 这种结构几乎与矢量结构完全一致。
表4-2 点状地物和结点的数据结构
| 点标识号 | M1 | M2 | 高程Z |
| … | … | … | … |
| 10025 | 43 | 4084 | 432 |
| 10026 | 105 | 7725 | 463 |
| … | … | … | … |
(2)线状地物的数据结构
一般认为用四叉树表达线状地物是困难的。但采用元子填满整条路径的方法,它的数据结构将变得十分简单。根据约定(2),线状地物有形状但没有面积,没有面积意味着线状地物和点状地物一样不必用一个完全的覆盖层分解四叉树,而只要用一串数据表达每个线状地物的路径即可,表达一条路径就是要将该线状地物经过的所有栅格的地址全部记录下来。 一个线状地物可能由几条弧段组成,所以应先建立一个弧段数据文件,如表4-3所示。
表4-3 弧段的数据结构
| 弧标识号 | 起始点号 | 终结点号 | 中间点串(M1,M2,Z) |
| … | … | … | … |
| 20078 | 10025 | 10026 | 58,7749,435,92,4377,439 |
| 20079 | 10026 | 10032 | 90,432,502,112,4412,496 |
| … | … | … | … |
表4-3中的起结点号和终结点号是该弧段的两个端点,它们与表4-2联接可建立弧段与结点间的拓扑关系。表中的中间点串不仅包含了原始采样点(已转换成用M1、M2表示),而且包含了该弧段路径通过的所有格网边的交点,它所包含的码填满了整条路径。为了充分表达线性地物在地表的空间特性,增加了高程Z分量。一条线性地物是在崎岖的地面上通过的,只有记录该曲线通过的DEM格网边上的交点的坐标和高程值才能较好地表达它的空间形状和长度。
虽然这种数据结构比单纯的矢量结构增加了一定的存储量,但它解决了线状地物的四叉树表达问题,使它与点状、面状地物一起建立统一的基于线性四叉树编码的数据结构体系。 这对于点状地物与线状地物相交、线状地物之间的相交以及线状地物与面状地物相交的查询问题变得相当简便和快速。
有了弧段数据文件,线状地物的数据结构仅是它的集合表示,如表4-4。
表4-4 线状地物的数据结构
| 线标识号 | 弧段标识号 |
| … | … |
| 30031 | 20078,20079 |
| 30032 | 20092,20098,20099 |
| … | … |
(3)面状地物的数据结构
根据对面状地物的约定,一个面状地物应记录边界和边界所包围的整个面域。其中边界由弧段组成,同样引用表4-4中的弧段信息面域信息则由线性四叉树或二维行程编码表示。
同一区域的各类不同地物可形成多个覆盖层,例如建筑物、耕地、湖泊等可形成一个覆盖层,土地利用类型、土壤类型又可形成另外两个覆盖层。这里规定每个覆盖层都是单值的, 即每个栅格内仅有一个面状地物的属性值。每个覆盖层可用一棵四叉树或一个二维行程编码来表示。为了建立面向地物的数据结构,做这样的修改:二维行程编码中的属性值可以是叶结点的属性值,也可以是指向该地物的下一个子块的循环指针,即用循环指针将同属于一个目标的叶结点链接起来,形成面向地物的结构。
图4-25是链接情况,表4-5、表4-6是对应的二维行程编码、带指针的二维行程码。表4-6中的循环指针指向该地物下一个子块的地址码,并在最后指向该地物本身。这样,只要进入第一块就可以顺着指针直接提取该地物的所有子块,从而避免像栅格数据那样为查询某一个目标需遍历整个矩阵,大大提高了查询速度。
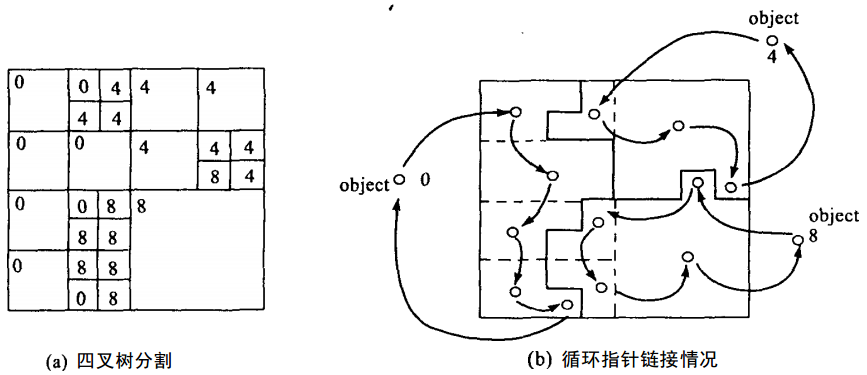
图4-25 链接情况
