当前位置:课程学习>>第八章 空间分析>>电子教案>>知识点三
知识点三:栅格数据分析
2. 邻域运算
邻域运算,涉及一个焦点像元和一组环绕像元。环绕像元是按其相对于焦点像元的距离和(或)方向性关系来选定的。常见的邻域类型有矩形、圆形、环形和楔形,如图8-16所示。矩形邻域是以像元为单位,有宽度和高度定义的,例如以焦点像元为中心的3×3窗口。圆形邻域则以焦点像元为圆心,以指定半径向外扩展。环形邻域是由以焦点像元为中心的一个小圆和大圆共同围成的环形区域组成。楔形邻域是以焦点像元为圆心的一片扇形。
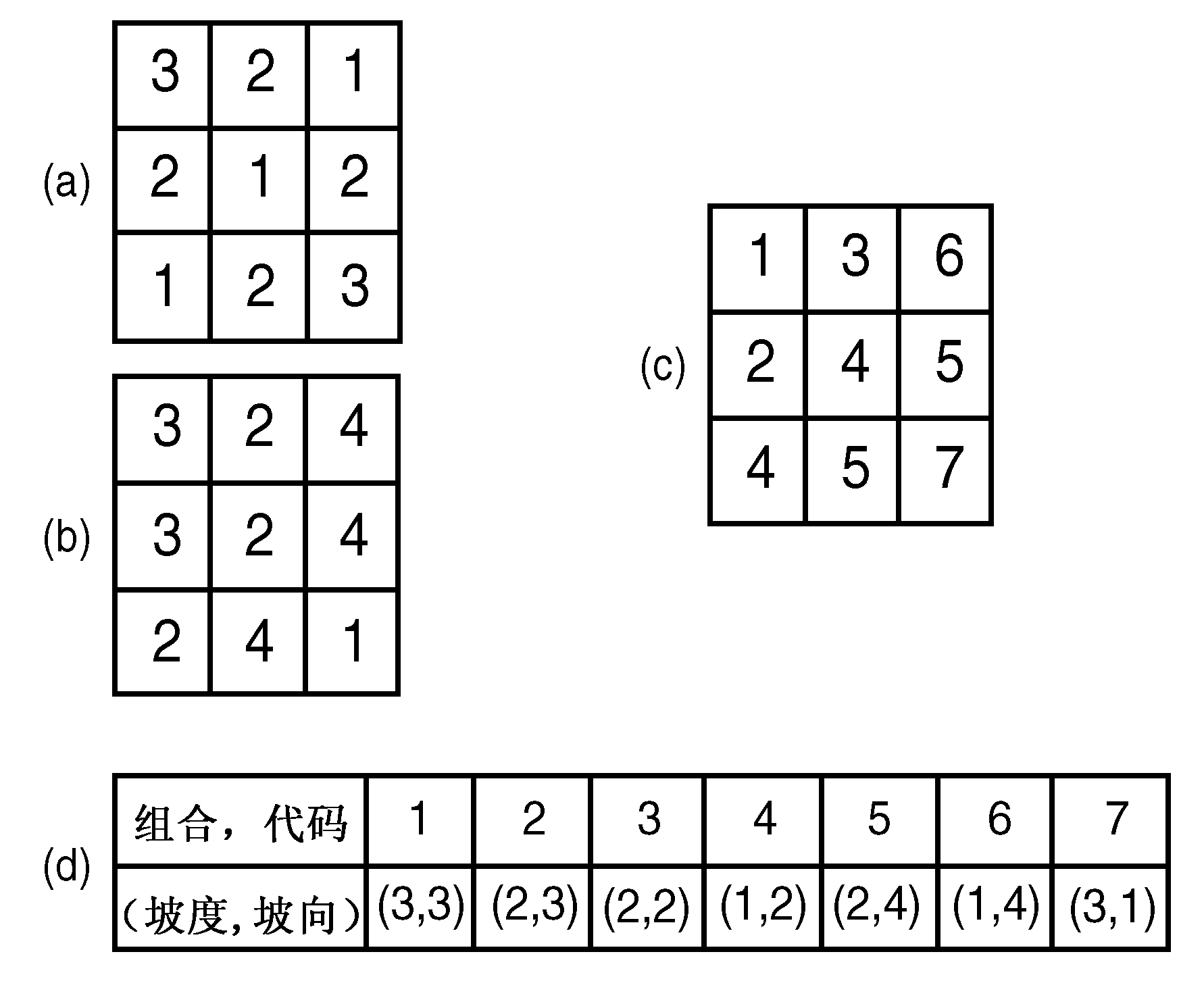
图8-15(c)中的每个像元值代表(a)和(b)像元值的独特组合。组合代码及其含义见
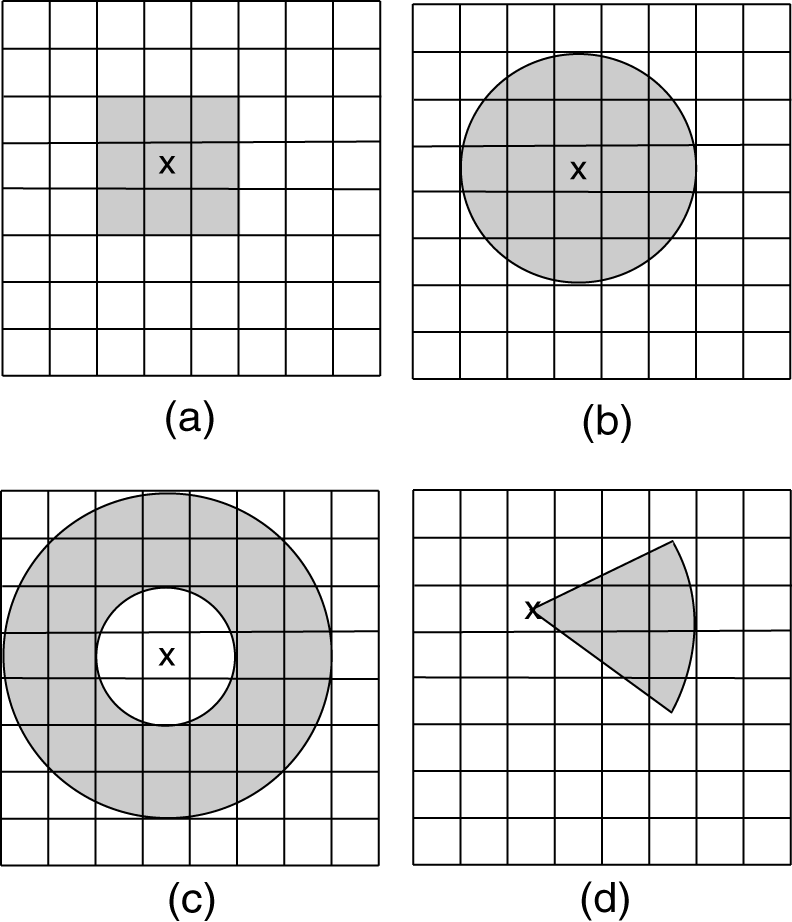
图8-16 四种常见的邻域类型:矩形(a)、圆形(b)、环形(c)和 楔形(d)。带 x 标记的像元为焦点像元
邻域运算通常用邻域内的像元值(包括或不包括焦点像元值)进行计算,然后将计算值赋予焦点像元。要完成一个栅格的邻域运算,需要将焦点像元从一个像元移到另一个像元,直到所有像元都被访问过。尽管邻域运算在单一栅格上进行,但其处理过程类似于多个栅格数据运算。不同的是,邻域运算使用定义的像元值,而不是用不同输入栅格的像元值。
从输出栅格看,邻域运算得到的既可以是最小值、最大值、值域、总和、平均值、中值、标准差等统计值,也可以是众数、少数和种类数等测量值列表。这些统计值和测量值与栅格局域运算的统计值和测量值相同。
邻域计算的一个重要应用是简化数据。例如,滑动平均减少了输入栅格像元值的波动水平。该方法采用矩形作为邻域空间。随着邻域从一个焦点像元移到另一个焦点像元,计算得出的邻域像元值的平均值并将其赋予该邻域的焦点像元。如图8-17所示。
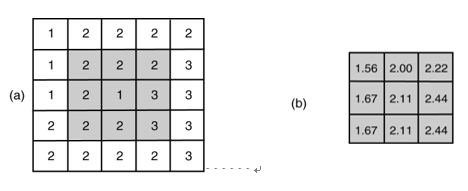
图8-17 中像元值是(a)中的阴影像元的以3×3为邻域的邻域平均值。例如,(b)中的 1.56是由(1 +2 +2 +1 +2 +2 +1 +2 +1)/9 计算得来
3. 分区运算
分区运算用于处理相同值或相似要素的像元分组,这些组称为分区。分区可以是连续的或不连续的。其中,连续分区包含的像元是空间上相连的,而非连续分区包含像元的分隔区。流域栅格是连续分区的一个例子,其中属于同一个流域的像元在空间上是相连的。土地利用栅格则是非连续分区的例子,土地利用的一个类型可以出现在栅格的不同区域。
分区运算可对一个或两个栅格进行处理。若为单一输入栅格,分区运算量测每个分区的几何特征,如面积、周长、厚度和重心,如图8-18所示。面积分区的像元数与像元大小的乘积。连续分区的周长就是其边界长度,而不连续分区的周长为每个分区的长度之和。厚度是计算在每个分区内可画的最大圆半径。重心是分区的几何中心,即与分区最匹配的椭圆长短轴的交点。
给定两个栅格(一个输入栅格和一个分区栅格),要求以分区栅格的区域为范围对输入栅格进行分区运算生成输出栅格,输出栅格对分区栅格的每个分区概括了输入栅格的像元值。概括统计值和量测值包括面积、最小值、最大值、总和、值域、平均值、标准差、中值、众数、少数和种类数。图8-19显示了按分区计算平均值的分区运算过程。

图8-18 两个大流域(分区)的厚度和重心。面积以km2表示,周长和厚度以km表示,每个分区的重心则标以x
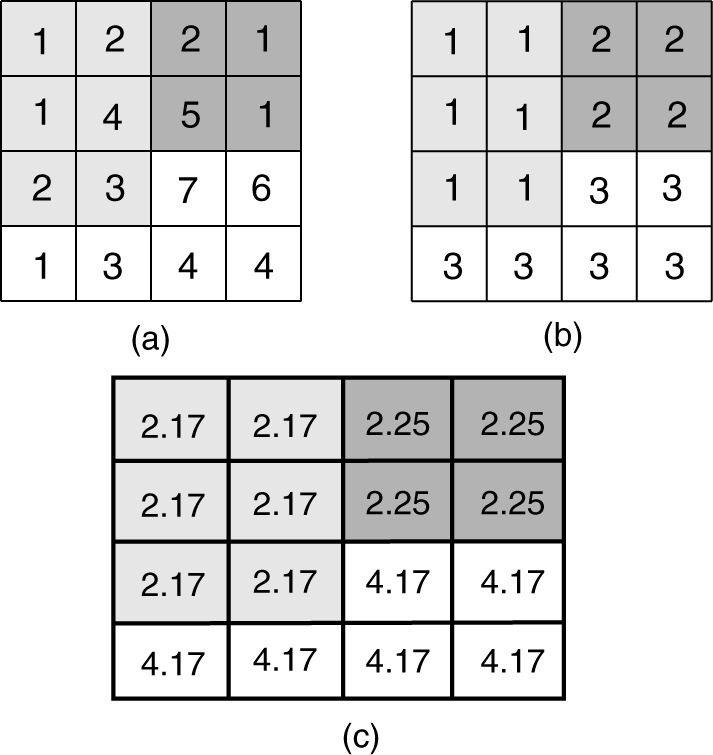
图8-19(c)中的像元值是由输入栅格(a)和分区栅格(b)运算的分区平均值。例如,2.17是分区1: {1, 1, 2, 2, 4, 3}的平均值
