当前位置:课程学习>>第八章 空间分析>>电子教案>>知识点四
知识点四:政策客体
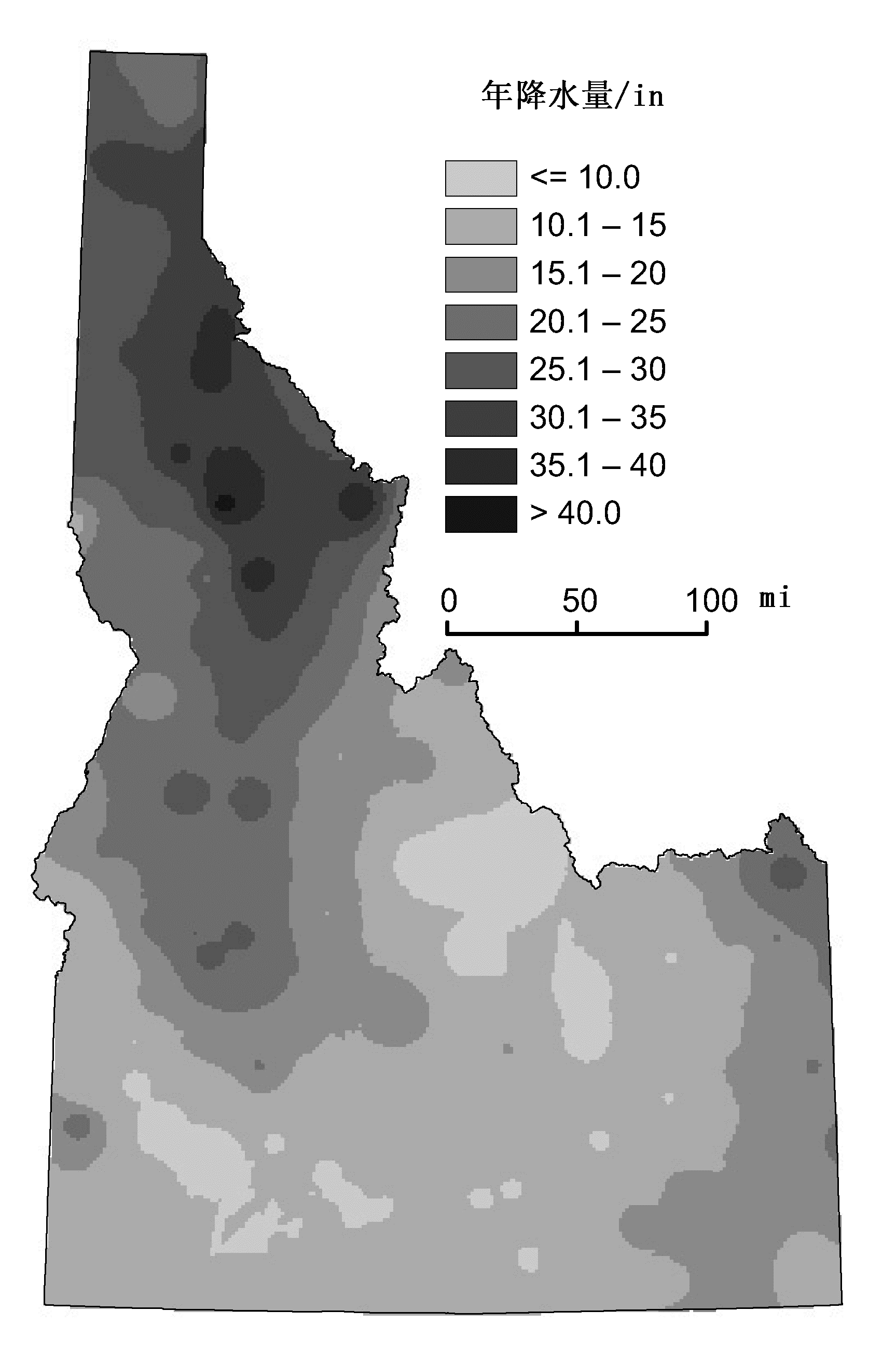
图8-23 基于距离倒数平方法生成的年平均降水量曲面
样条函数是分段函数,每次只用少量数据点,故插值速度快。样条函数与趋势面分析和移动平均方法相比,它保留了局部的变化特征。线性和曲面样条函数都在视觉上得到了令人满意的结果。样条函数的一些缺点是:样条内插的误差不能直接估算,同时在实践中要解决的问题是样条块的定义以及如何在三维空间中将这些“块”拼成复杂曲面,又不引入原始曲面中所没有的异常现象等问题。
克里金插值
前面介绍的几个插值方法对影响插值效果的一些敏感性问题仍没有得到很好的解决,例如趋势面分析的控制参数和距离倒数插值方法的权重对结果影响很大,这些问题包括:需要计算平均值数据点的数目;搜索数据点的邻域大小、方向和形状如何确定;有没有比计算简单距离函数更好的估计权重系数的方法;与插值有关的误差问题。
为解决这些问题,法国地理数学家Georges Matheron和南非矿山工程师D.G.Krige研究了一种优化插值方法,用于矿山勘探。这个方法被广泛地应用于地下水模拟、土壤制图等领域,成为GIS软件地理统计插值的重要组成部分。这种方法充分吸收了地理统计的思想,认为任何在空间连续性变化的属性是非常不规则的,不能用简单的平滑数学函数进行模拟,可以用随机表面给予较恰当的描述。这种连续性变化的空间属性称为“区域性变量”,可以描述象气压、高程及其它连续性变化的描述指标变量。这种应用地理统计方法进行空间插值的方法,被称为克里金(Kriging)插值。地理统计方法为空间插值提供了一种优化策略,即在插值过程中根据某种优化准则函数动态的决定变量的数值。Matheron,Krige等人研究的插值方法着重于权重系数的确定,从而使内插函数处于最佳状态,即对给定点上的变量值提供最好的线性无偏估计。
克里金插值方法的目的是提供确定权重系数最优的方法和并能描述误差信息。由于克里金点模型(常规克里金模型)的内插值与原始样本的容量有关,当样本少的情况下,采用简单的点常规克里金插值的内插结果图会出现明显的凹凸现象。可以通过修改克里金方程以估计子块内的平均值来克服这一缺点。该方法叫块克里金插值,该方法对估算给定面积试验小区的平均值或对给定格网大小的规则格网进行插值比较适用。块克里金插值估算的方差结果常常小于点克里金插值,所以生成的平滑插值表面不会发生点模型的凹凸现象。
