当前位置:课程学习>>第十二章 遥感数字图像处理>>电子教案>>知识点二
知识点二:遥感图像预处理
2.2.2 遥感图像几何校正
遥感图像的几何校正(Geometric Correction)是指从具有几何畸变的遥感图像中消除畸变的过程,即定量地确定图像上像元坐标与目标物的地理坐标间对应关系(坐标变换式)的过程(图1-9)。
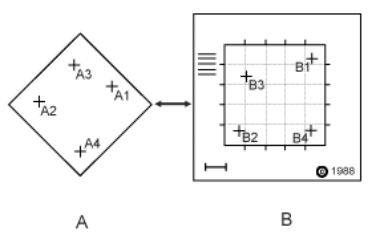
图1-9几何校正的示意
1.几何校正的基本思路
校正前的图像看起来是由行列整齐的等间距像元点组成,实际上,由于某种几何畸变,图像中像元点间所对应的地面距离并不相等(图1-10)。校正后的图像亦是由等间距的网格点组成的,且以地面为标准,符合某种投影的均匀分布,图像中格网的交点可以看作是像元的中心。校正的最终目的是确定校正后图像的行列数值,然后找到新图像中每一像元的亮度值。
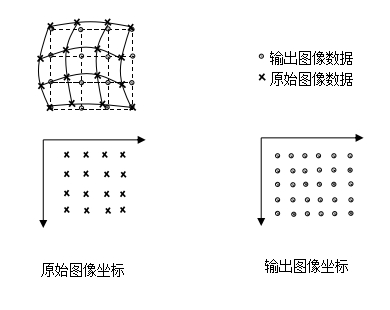
图1-10 遥感图像几何校正
具体校正步骤如图1-11:
(1)确定校正方法。考虑到图像中所含几何畸变的性质及可应用于校正的数据,确定校正的方法;
(2)确定校正的公式。确定校正公式(图像坐标和地图坐标的变换公式等)的结构,根据控制点数据等求出校正公式的参数;
(3)验证校正的方法、校正公式的有效性。检查几何畸变能否充分得到校正,探讨校正公式的有效性。当判断无效时,则对新的校正公式进行探讨,或对校正中所用的数据进行修改;
(4)重采样、内插。为使校正后的输出图像的配置与输入图像相对应,利用校正公式对输入图像的数据重新排列。在重采样中,由于所计算的对应位置的坐标不是整数值,所以必须通过对周围的像元值进行内插,以求出新的像元值。
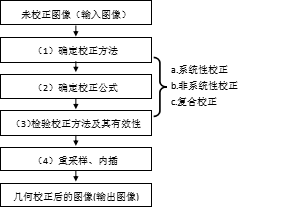
图1-11 几何校正过程
2.几何校正过程
(1)地面控制点(GCP)选取
选好地面控制点是保证几何精校正质量的基础。地面控制点应具有以下特征:
① 地面控制点在图像上有明显的、清晰的定位识别标志,如道路交叉点、河流叉口、建筑边界、田块田界线、桥头等;
② 地面控制点上的地物不随时间而变化,以保证当两幅不同时段的图像或地图几何校正时,可以同时识别出来;
③ 在没有做过地形校正的图像上选控制点时,应尽可能在同一地形高度上进行。
④ 地面控制点(GCP)应当均匀分布在整幅图像内,且要有一定的数量保证,否则会在GCP密集区几何校正精度较高, GCP分布稀疏区将出现较大的拟合误差。
控制点的精度和选取的难易程度与图像的质量、地物的特征及图像的空间分辨率密切相关。对于一般齐次多项式,GCP的个数至少不得低于多项式的系数个数。适当增加GCP的数量,可以提高几何校正的精度,但过多的GCP不但不会显著提高校正精度,而且会增大选择GCP的工作量,有时甚至难以选出大量的GCP。如一幅TM影像要校正到一个像元以内的精度,一般需要30个左右均匀分布的GCP;一幅SPOT卫星影像采用三次多项式拟合,用13至17个GCP,其校正精度可达到两个像元左右。
初选控制点后还需进行控制点匹配精度的检验,即利用公式(1-8)计算每个地面控制点的均方根误差(RMSerror)。
(1-8)
其中,X、Y是地面控制点在原图像中的坐标,x、y是对应于相应的多项式计算的控制点坐标,估算坐标和原来坐标之间的差值大小代表了每个控制点几何校正的精度。通常用户会指定一个可以接受的最大总均方根误差(误差限额一般定义为0.5,至多一个像元),如果控制点的实际总均方根超过这个阈值,则需要剔除那些匹配误差超限的控制点或选取新的控制点。如此反复,直到达到所要求的精度为止。
(2)图像空间变换
在地面控制点确定以后,应该在图像和地图上分别读出各个控制点在图像上的像元坐标(x, y)及其参考图像或地图上的坐标(X, Y)。
直接法坐标变换(多项式校正法)是在实践中解决此类问题的一种比较好的方法,特别适合于地面相对平坦地区的图像校正。该法的基本思想是回避成像的空间几何过程,而直接对图像变形的本身进行数学模拟。在图像平移、缩放、仿射、偏扭、弯曲以及更高次的基本变形的基础上,确定表达校正前后图像相应点之间的坐标关系多项式。该法适用于各种类型的传感器校正,图像对地面(或地图)系统的校正以及为满足计算机分类、地物变化监测等处理而进行的不同类型遥感图像之间的相互几何配准。从原始图像阵列出发,依次对其中每一个像元分别计算其在输出(校正后)图像的坐标:

(1-9)
即:
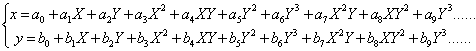
(1-10)
其中,x、y为某像元的原始图像坐标;X、Y为校正后同名点的地面(或地图)坐标;ai、bi为多项式系数(i = 0, 1, 2, …)。
可以看出,只要求解出ai、bi这两组系数就可以直接利用式(1-10)进行校正。在通常情况下,这些多项式系数常利用所选的控制点坐标,按最小二乘法回归求得。
(3)数字图像重采样、内插
重新定位后的像元在原图像中分布是不均匀的,即输出图像像元点在输入图像中的行列号不是或不全是整数关系,不能简单地用原图像像元灰度值代替输出图像像元灰度值,必须通过适当的方法把该点四周邻近的若干个整数点上的像元灰度值对该点的灰度值贡献累积起来进行计算,这个过程称为数字图像的重采样(Resampling)(图1-12)。
