当前位置:课程学习>>第十三章 遥感信息提取>>电子教案>>知识点二
知识点二:计算机分类
遥感图像分类处理中,应用最广且比较简单的距离函数有欧几里得距离和绝对距离(混合距离)两种,但一般采用欧氏距离,即
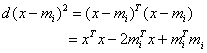 (1-1)
(1-1)
其中,i=1, 2, …, M
判别准则为:x∈wi,if , for all j≠i
式(1-1)中,xTx对所有类别均相同,可不予考虑,此时判别准则简化为:
x∈wi, if ![]() . for all j≠i
. for all j≠i
其中, ![]() (1-2)
(1-2)
尽管最小距离法与其他监督分类算法相比比较简单,但其应用并不广泛,其主要缺点是此方法没有考虑不同类别内部方差的不同,从而造成一些类别在其边界上的重叠,引起分类误差,因此需要一些更高级复杂测量距离的方法。
2、费歇尔(Fisher)线性判别分类法
采用统计学中的费歇尔准则对遥感图像进行自动识别分类称为费歇尔线性判别分类。费歇尔准则是指依据类间均值方差与类内方差总和之比为极大的决策规则,即“类间最大分离”的准则,它要求类间距离最大,即类间均值差异最大,而类内的离散性最小,即方差平方和最小。这种方法与最小距离分类的思想是一致的,但是它借以判定类别的不是距离,而是通过建立线性判别函数加以实现。
现以简单的二维图像判别两类地物情况为例,如图1-6所示,有两类地物A、B,在x1和x2轴方向上的投影均有不同程度的重叠,所以彼此不能很好地区分。但如果找到一条直线R为坐标轴,使得A、B两类的中心在R上的投影点间距线段最长,即两类的均值差异达到最大,在R轴上的投影没有重叠,这时通过中点R0的垂直线L就能把两类地物的点群分开,此线就称为线性判别函数,其表达式为
R=S1x1+ S2x2 (1-3)
其中,S1、S2是待解的系数,x1和x2是任意像元X的两个变量。当某像元X的各波段灰度值代入上式时,就可以得到该像元的判别函数值R=g(x),为了使各类的R值有明显判别,x1和x2可以是原始值,也可以是经过某种变换的新数据(但需注意,Fisher线性判别是以多维正态分布为基础,有些特征变量,如波段比值等,不是正态分布应进行变换后才能使用)。为了建立上述方程,首先需要采样训练,再以所有训练样本计算两类平均判别函数值
![]() (1-4)
(1-4)
R0值就是区分A、B两类地物的标准,R>R0为一类,R<R0为另一类。R0称为判别指数,其几何意义就是图1-6中的判别直线L,R为判别值。
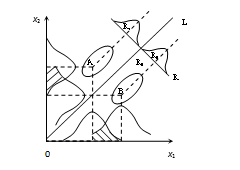
图1-6 二维变量判别原理
依据Fisher线性判别函数进行的遥感图像自动识别分类,在平坦地区,并且训练样本多时,可望取得较好的分类结果。
3、最大似然比分类法(Maximum Likelihood Classifier)
建立在贝叶斯准则基础上的最大似然分类法与最小距离分类法相比更加成熟,是监督分类中常用的且精度较高的一种算法。它是求出遥感数字图像中各像元数据对于各类别的似然度,然后将该像元归到似然度最大类别中去的方法。设从类别k观测到x的条件概率为p(x|k),则似然度Lk为
![]() (1-5)
(1-5)
其中,x为待分像元,p(k)为类别k的先验概率,它可以通过训练区来决定。此外,由于式(7.22)中分母和类别无关,在类别间比较的时候可以忽略。从数学角度来说,最大似然判别分类是至今发展出的一种最好的分类方法,因为它还考虑到判别风险问题。
现定义一组代价函数(或称损失函数、风险函数)λ(l/k)来表示错判应付出的代价,其中l或k=1, 2, …, G,λ(l/k)构成一个矩阵形式的代价表:
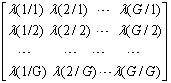
代价表中的任意元素λ(l/k)反映k类像元错分为一类所引起的损失或付出的代价。判别一个像元属于哪一类都要冒一定的风险,即要付出一定的代价,只是大小不同,能将待判别像元归属到付出代价最小的那一类中为最好,这就是贝叶斯的最优化规则。为此就要在全部可能的分类类别中找出平均代价最小的类别,设L1(X)为像元X判成一类的平均最小代价,代价函数L1(X)只能是λ(l/k)的平均,k=1, 2, …, G,而且这个平均是加权情况下的平均。因此,对于一个给定像元X,判别它来自一类所引起的平均代价为
![]() (1-6)
(1-6)
其中,用像元X归属k类的条件概率P(k/X)作为代价函数的权函数。结合式(1-6)有
![]() (1-7)
(1-7)
其中,![]() 。
。
为了便于用平均代价函数L1(X)作为判别函数,需先明确下面三条规则:
① 求一个函数集的最小,等于对同一函数集取负号后求最大;
② 一组合理的特殊代价值:
当l=k时,λ(l/k)=0,此时代价或风险为零;
当时,λ(l/k)=1,此时代价或风险最大。
正确的分类无需付出代价,损失为零,而错误的分类则付出最大的代价。
③ 若Hl(X)(l=1, 2, …, G)是一个判别函数集,则任何单调函数应用到这个集合,都会产生等价的判决函数集。即无论使用哪一个函数集,都将会产生同样的分类结果。
特别地,在最大似然比分类法中,要求各波段之间的相关性较小,各变量呈正态分布,并且训练样本个数至少要为N+1个,(N为特征空间的维数),这样才能保证协方差矩阵的非奇异性。因而通常在利用最大似然比分类法前应考虑波段选择问题,或是对遥感图像进行K-L变换等。一般训练样本像元数应10倍于波段数N,当要获得较高的分类精度时,须使用100倍于波段数N的训练样本。
