当前位置:课程学习>>第一章 代数运算与数学归纳法>>学习内容>>视频课堂>>知识点二
知识点二:第一数学归纳法
数学归纳法是数学证明中一个重要的方法。数学归纳法所根据的原理是正整数集的一个最基本的性质——最小数原理。
用![]() 表示非负整数集合:
表示非负整数集合:![]() , 用
, 用![]() 表示整数集合,用
表示整数集合,用![]() 表示正整数集合。
表示正整数集合。
最小数原理:正整数集![]() 的任意一个非空子集
的任意一个非空子集![]() 必含有一个最小数,即存在一个数
必含有一个最小数,即存在一个数![]() ,使得对任意的数
,使得对任意的数![]() ,都有
,都有![]() 。
。
如 ![]() ,
,![]() 都是
都是![]() 的非空子集,
的非空子集,![]() 分别有最小数为5,1000。
分别有最小数为5,1000。
注意1. 最小数原理并不是对于任意数集都成立的。例如,全体整数集合![]() 就没有最小数。又如,全体正分数所成的集合也没有最小数。这是因为如果
就没有最小数。又如,全体正分数所成的集合也没有最小数。这是因为如果![]() 是正分数,那么
是正分数,那么![]() 就是小于
就是小于![]() 的正分数。
的正分数。
2. 设![]() 是一个整数。令
是一个整数。令
![]()
那么以![]() 代替正整数集
代替正整数集![]() ,最小数原理对于
,最小数原理对于![]() 仍然成立。也就是说,
仍然成立。也就是说,![]() 的任意一个非空子集必含有一个最小数。特别地,
的任意一个非空子集必含有一个最小数。特别地,![]() 的任意一个非空子集必含有一个最小数。
的任意一个非空子集必含有一个最小数。
由最小数原理可以给出第一数学归纳法。
定理1.2.1(第一数学归纳法)设有一个与正整数![]() 有关的命题
有关的命题![]() 。如果
。如果
⑴ 当![]() 时,
时,![]() 成立;
成立;
⑵ 假设![]() 时,
时,![]() 成立,则当
成立,则当![]() 时,
时,![]() 也成立,那么
也成立,那么![]() 对一切正整数
对一切正整数![]() 都成立。
都成立。
证明:用反证法。假设命题![]() 不是对一切正整数都成立,令
不是对一切正整数都成立,令![]() 表示使
表示使![]() 不成立的正整数组成的集合, 那么
不成立的正整数组成的集合, 那么![]()
![]() 。由最小数原理,
。由最小数原理,![]() 中有最小数
中有最小数![]() 。 因为当
。 因为当![]() 时,
时,![]() 成立,所以
成立,所以![]() ,从而
,从而![]() 是一个正整数。因为
是一个正整数。因为![]() 是
是![]() 中最小数,
中最小数,![]() 。即当
。即当![]() ,
,![]() 成立。于是由⑵知,当
成立。于是由⑵知,当![]() 时,
时,![]() 成立。因此
成立。因此![]() 。这是一个矛盾。
。这是一个矛盾。
理解数学归纳法的定义和正确性并不难,但是要正确地用好数学归纳法却不是一件容易的事。
数学归纳法中的两步缺一不可。验证![]() 成立是基础,利用归纳法假设结合已知的有关数学知识证明
成立是基础,利用归纳法假设结合已知的有关数学知识证明![]() 成立是递推的根据。这两步对证明命题相辅相成,构成数学归纳法证明过程的逻辑结构。尤为重要的是在证明过程中必须用到归纳假设,这是检验是否用对了数学归纳法的一把尺。
成立是递推的根据。这两步对证明命题相辅相成,构成数学归纳法证明过程的逻辑结构。尤为重要的是在证明过程中必须用到归纳假设,这是检验是否用对了数学归纳法的一把尺。
例1.2.1 证明:对任意![]() , 都有
, 都有
![]() (1.2.1)
(1.2.1)
证明:当![]() 时,
时,![]() 式右边
式右边![]() ,左边
,左边![]() ,故
,故![]() 时,
时,![]() 式成立。
式成立。
现设![]() 式对
式对![]() 成立,考虑
成立,考虑![]() 的情形,
的情形,
利用 ![]() ,知
,知
![]()
![]()
![]()
![]()
![]()
![]()
所以,![]() 式对
式对![]() 成立。
成立。
综上,由数学归纳法原理知![]() 式对一切正整数n都成立。
式对一切正整数n都成立。
说明: 这是一个错误的证明,其错误在于证明![]() 对
对![]() 成立时,并没有用到归纳假设。
成立时,并没有用到归纳假设。
正确的过程如下:由归纳假设知
![]()
![]()
![]()
![]()
![]()
![]()
![]()
事实上![]()
![]() 式的得到是正确的,但是是对
式的得到是正确的,但是是对![]() 式的一个直接证明,不应该套上数学归纳法这顶帽子。这一点也是初学者经常犯的一些错误,应认真改正,否则难以形成一个正确的逻辑推导的思维过程。
式的一个直接证明,不应该套上数学归纳法这顶帽子。这一点也是初学者经常犯的一些错误,应认真改正,否则难以形成一个正确的逻辑推导的思维过程。
例1.2.2 证明![]()
证明:假设![]() 时,命题正确,即
时,命题正确,即![]()
当![]() 时,
时,
![]()
![]()
![]()
![]()
![]()
即命题对![]() 正确。因此,对任意自然数
正确。因此,对任意自然数![]() 都是正确的。
都是正确的。
事实上,![]()
显然命题是错误的,而证明过程中忽略了数学归纳法的第一步,才导致了错误的结论。
例1.2.3 求证:![]()
证明:当![]() 时,上式显然成立.
时,上式显然成立.
假设![]() 时成立,考虑
时成立,考虑![]() 情形
情形
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
所以对![]() 时也正确。因此,命题对一切自然数
时也正确。因此,命题对一切自然数![]() 都成立。
都成立。
例1.2.4 求证:![]() 个正实数的算数平均值大于或等于这
个正实数的算数平均值大于或等于这![]() 个数的几何平均值,即
个数的几何平均值,即
![]()
![]()
其中![]() 。
。
证明:当![]() 时,显然成立;当
时,显然成立;当![]() 时,
时,![]() 式等价于
式等价于![]() ,即
,即![]() ,故
,故![]() 式成立。
式成立。
假设![]() 式对
式对![]()
![]() 成立,考虑
成立,考虑![]() 情形
情形
记 ![]() ,
,
由归纳假设知
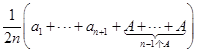
![]()
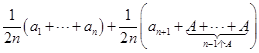
![]()
![]()
![]() 。
。
注意到![]() ,故
,故
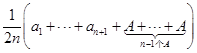
![]()
![]() ,
,
所以 ![]() ,
,
进而,![]() ,即
,即
![]()
故![]() 对
对![]() 成立。所以,对任意自然数
成立。所以,对任意自然数![]() ,不等式(1.2.3)成立。
,不等式(1.2.3)成立。
注意: 根据最小数原理及上面的注意2,我们可以取![]() 来代表正整数集
来代表正整数集![]() 。也就是说,如果某一个命题是从某一个整数开始成立,这时仍然可以利用数学归纳法来证明,只要把定理1.2.1中条件 ⑴
。也就是说,如果某一个命题是从某一个整数开始成立,这时仍然可以利用数学归纳法来证明,只要把定理1.2.1中条件 ⑴ ![]() 换成
换成![]() 即可。
即可。
例1.2.5 证明:当![]() 时,
时,![]() 边形的内角和等于
边形的内角和等于![]() 。
。
证明:当![]() 时,命题成立。因为三角形内角和等于
时,命题成立。因为三角形内角和等于![]() 。
。
假设![]()
![]() 时命题成立,看任意一个
时命题成立,看任意一个![]() 边形
边形![]() (如图1.2.1)。
(如图1.2.1)。
联结![]() ,那么
,那么![]() 的内角和等于三角形
的内角和等于三角形![]() 的内角和与
的内角和与![]() 边形
边形![]() 的内角和之和。
的内角和之和。
前者和为![]() ,后者归纳假设为
,后者归纳假设为![]() 。
。
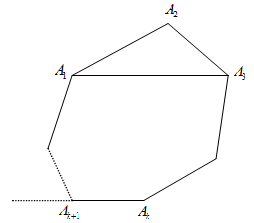
图1.2.1
因此![]() 边
边![]() 内角和为
内角和为
![]() 。所以对任意的正整数
。所以对任意的正整数![]()
![]() ,结论成立。
,结论成立。
