定义1.1.1 设是两个集合，作一个新集合

称这个集合是与的笛卡尔积，记作。

注意：是一个元素对，因而

=

一般说来，并不等于。例如，设，，则

，

。

然而，当都是有限集时，，所包含元素个数是相同的，都等于（ 表示集合的元素个数）。

我们知道数的加、减、乘、除运算；多项式的加、减、乘运算都具有一个共同的特点，即两个得唯一的一个。换句话说，对任意取定的两个元素，按照某种法则都有唯一确定的一个元素与之对应。于是有如下定义

定义1.1.2 设是三个非空集合，称映射是到的代数运算。特别地，当时，映射称为上的二元代数运算。

一个代数运算可以用“”来表示，并把在“”下的象记为.

例1.1.1 设是实数集，映射

是上的二元代数运算。用约定记法写为，这就是通常的实数加法。

例1.1.2  在阶方阵集合上，规定二元代数运算

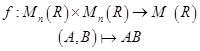
写为，它是通常矩阵乘法。

例1.1.3  设，规定二元代数运算

偶偶偶，偶奇奇

奇偶奇，奇奇偶

则是上的一个二元代数运算。

在整数集合中，加、减、乘都是上的二元代数运算，但除法不是的二元代数运算，因为。同样，在多项式集合中，多项式的加法、减法、乘法都是上的二元代数运算，但除法不是上的代数运算。因为。