当前位置:课程学习>>第一章 代数运算与数学归纳法>>学习内容>>文本学习>>知识点三
知识点三:第二数学归纳法
在有些情况下,归纳法假定“命题![]() 对于
对于![]() =
=![]() 成立”还不够,而需要较强的假定。
成立”还不够,而需要较强的假定。
定理1.2.2 (第二数学归纳法)设有一个与正整数![]() 有关的命题
有关的命题![]() 。如果
。如果
⑴ 当![]() 时,
时,![]() 成立;
成立;
⑵ 假设对于![]() <
<![]() 的自然数
的自然数![]() 成立,则
成立,则![]() 时,
时,![]() 也成立。
也成立。
那么![]() 对一切自然数都成立。
对一切自然数都成立。
证明:考虑命题![]() :“对所有
:“对所有![]() ,
,![]() 都成立。”则由
都成立。”则由![]() 成立,可知
成立,可知![]() 成立。
成立。
当![]() 时,由 ⑴ 知
时,由 ⑴ 知![]() 成立,从而
成立,从而![]() 成立。
成立。
假设![]()
![]() 成立,即对所有
成立,即对所有![]() ,
,![]() 都成立,则 ⑵ 知
都成立,则 ⑵ 知![]() 成立,所以对
成立,所以对![]() ,
,![]() 成立,从而
成立,从而![]() 成立。于是由第一数学归纳法可知对任意
成立。于是由第一数学归纳法可知对任意![]() ,
,![]() 都成立,进而
都成立,进而![]() 成立。
成立。
第二数学归纳法是第一数学归纳法的推论。在作归纳假设时,我们假设了![]() 都成立,并在此前提下证出
都成立,并在此前提下证出![]() 成立,这是区别于第一数学归纳法的地方,有时会给证明带来很大的方便。
成立,这是区别于第一数学归纳法的地方,有时会给证明带来很大的方便。
另外,第二数学归纳法也可仿照第一数学归纳法用反证法去证明。
例1.2.6 证明Fibonacci(L.斐波那契)数列
![]()
的通项公式为
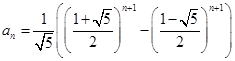
证明:当![]() 时,
时,
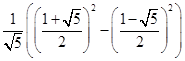
![]()
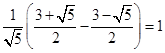
命题成立。
假设![]() 时公式成立,现证
时公式成立,现证![]() 时公式也成立。此时
时公式也成立。此时
![]()
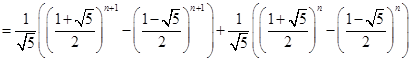
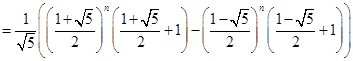
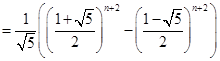
即公式成立。所以对任意自然数公式都成立。
例1.2.7 数列![]() 满足
满足![]() ,且
,且
![]() (1.2.4)
(1.2.4)
![]() (1.2.5)
(1.2.5)
![]() 证明:
证明:![]() 是完全平方数。(2000年全国高中数学联赛试题)。
是完全平方数。(2000年全国高中数学联赛试题)。
证明:由(1.2.4)得![]() ,代入(1.2.5)后整理得
,代入(1.2.5)后整理得
![]() 。
。
于是
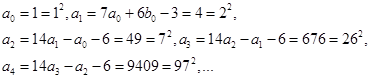
由此我们猜想![]()
下面我们用数学归纳法证明这一猜想成立。
![]() 时,
时,![]()
设![]() 时,
时,![]() 时,
时,![]() 那么,
那么,
![]()
![]()
![]()
其中
![]()
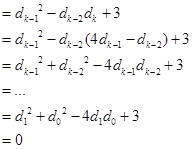
所以![]() 这就证明了对一切非负整数
这就证明了对一切非负整数![]() ,
,![]() 是完全平方数。
是完全平方数。
通过以上几例证明应用数学归纳法两个步骤缺一不可,如果是猜想,必须用数学归纳法去证明,而猜想是否正确,推证一千次,一万次,也不一定正确的。
例1.2.8费马(Fermat)猜想式子![]() 的值是素数。
的值是素数。
事实上,当![]() 的时候,其值分别等于3,5,17,257,65537,这5个数都是素数,由于没有用数学归纳证明,这只能是猜想。后来欧拉(Euler)举出当
的时候,其值分别等于3,5,17,257,65537,这5个数都是素数,由于没有用数学归纳证明,这只能是猜想。后来欧拉(Euler)举出当![]() 时,
时,![]() ,因而费马这个猜想是错的。
,因而费马这个猜想是错的。
