讲二个问题：（1）数域的概念；（2）一元多项式的概念

（1） 数域  

根据所研究的问题，我们常常需要明确规定和考虑数域的范围.例如我们分别用表示自然数，整数，有理数，实数与复数的集合,并且

在复数集中有加法,减法,乘法与除法四种运算,称为四则运算.

为了方便，我们引入一些术语

设是复数集的一个子集,如果对任何，有（“”可以是的加法，减法，乘法和除法（除法时分母不为）），则称对“”运算封闭。

例2.2.1 对加法与乘法封闭，但对减法与除法（除法时分母不为）不封闭。

例2.2.2 对加,减,乘,除法（除法时分母不为）都封闭。

定义2.2.1 设是复数集的非空子集，如果满足条件：

（1）；

（2）对四则运算都封闭，

则称是一个数域。

由例2.2.1知道，不是数域。由例2.2.2知道，都是数域,分别称为有理数域,实数域,复数域。

例2.2.3 设, 则是一个数域。

证明  因为,故满足条件（1）。

设,

则

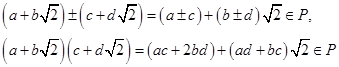
又设则至少有一个不为0，从而。

于是，

从而是一个数域。

显然

命题2.2.1   若是一个数域，则。

证明  因为是数域，故, 由的封闭性知。.

（2）一元多项式的概念

一元多项式的运算是大家熟知的，本节作一个简单的介绍，在这章里总假设是某个数域，是一个符号（也称不定元，读者不妨把它看成一个变量）

定义2.2.2  设是一个非负整数，形式表达式

             (2.2.1)

称为系数在数域中的一元多项式，或称为数域上的一元多项式。

称为次项，称为次项的系数；称为常数项；若，则称是首项（最高项），为首项系数，而称为该多项式的次数，记为。

若多项式中各项系数全为零，称此多项式为零多项式，记为，规定零多项式的次数为，的运算规则如下:

+所有整数=， +=，＜任何整数。

零次多项式就是一个非零常数  。

我们把上所有一元多项式的集合记为，用或等符号表示一元多项式。

定义2.2.3  上两个多项式称为相等，如果它们的各项系数都对应相等，即

此时，记为

下面讨论中加法，减法和乘法运算

定义2.2.4 中多项式的和定义为 。

例2.2.4设，则

。

容易验证加法有下列运算规律

加法结合律：

(1)；

(2)加法交换律；

(3)；

(4)设记，则

称为的负多项式，并且有

                           。

有了负多项式的概念就可以定义多项式的减法

定义2.2.5 中多项式的差定义为。

即。

定义2.2.6 中多项式的积定义为

             。

如果记，其中

例2.2.5 设,则。

容易证明乘法有下面的运算规律

(1)乘法结合律： ；

(2)乘法交换律  ；

(3)；

(4)乘法对加法的分配律

；

。

以后把数域上一元多项式的全体称为一元多项式环。

命题2.2.2

（1）对多项式的加法，有

；

（2）对于多项式的乘法，有

；

（3）当且仅当或。

推论2.2.3 多项式的乘法满足消去律：如果且那么。

证明 移项后有

由命题2.2.2知道，由可以推出这也就是。

边学边练

1.举出对加法，乘法封闭，但对减法不封闭的例子。

2.问下列数集是否是数域

(1)全体偶数集；（2）全体正实数集；（3） 

3.计算多项式与g的和与乘积。

4.设，，

试确定使得。