数域上的一元多项式环中，可以做加法与乘法的运算，并且可以做加法的逆运算：减法，但是乘法的逆运算：除法却并不是的运算，因为两个多项式相除所得的结果不一定是多项式。什么样的两个多项式相除仍为多项式？这是我们关心的问题：为此先讨论两个多项式相除的一般情形，在中学数学中，讲过多项式的长除法，我们利用长除法可以求得一个多项式去除另一个多项式的商式和余式。

例如，设,      。

我们按下面的格式来作除法：

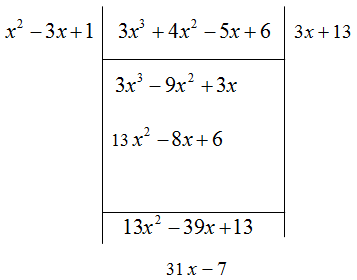
于是求得商式为,余式为所得结果可以写成

。

这个求法具有一般性，即一元多项式环具有下述重要性质。

定理2.3.1（带余除法） 设是两个多项式，其中则存在中唯一的一对多项式及使得

                      (2.3.1)

成立，其中＜（包括情形），称为被除的商式，称为被除的余式.

证明  存在性 对 运用归纳法证明与的存在性

    设，当时，是零次多项式，只须取，结论成立. 故设＞0，当＜时，只需取结论也成立。

现在假设，并假设当的次数小于时存在性已经成立.现在看的次数为的情形。

设和的首项分别是与，则的首项是.

从而

                    (2.3.2)

的次数小于对应用归纳假设，中存在使得

＜ ，            （2.3.3）

代入（2.3.2）得

。

只需取则得（2.3.1）式,应用归纳法原理就证明了定理的存在性部分。

唯一性  设另有多项式，使得

，

其中＜，于是

，

即

。

如果，则由可以得出，结论成立。

故可设由命题2.2.2（2）的次数公式,得到

，

这与假设＜矛盾， 唯一性得证。

我们感兴趣的是余式为零的情形.

定义2.3.1 设，若存在一个 使得

                                     (2.3.4)

则称整除，记作当整除时，称为的因式，称为的倍式.

当时，带余除法给出了整除性的一个判别法

定理2.3.2 设，且则的充分必要条件是除的余式为零。

证明  如果除的余式为零，则即。

如果，则有，使得

根据带余除法的唯一性得，除的余式为零。

根据整除的定义，可获得一元多项式整除的基本性质：

（1），零次多项式 能整除任意多项式： 

证明  由可知，由 可得

（2），当且仅当存在，使得。

把相差一个非零常数倍的多项式与（）称为相伴多项式。

证明 （）由假设可知存在多项式使得

 ,

从而

.

如果则=0，结论成立，若利用消去律得到

。

比较次数得  ，

因而从而于是

。

设，则有，又由可得 。

（3）若，，则。

证明 由假设可知存在多项式使得

.

因此

,

可知。

（4）若则对任意的有

。

证明 由，得

       =,

所以

（5）多项式的整除性与系数所在域的扩张无关。

设  都是数域.设, ，除的商式和余式，也是在中除的商式和余式。因此在中当且仅当在中.

例如  和都是整系数多项式，因此可以同时被看成 中多项式。然而不论将它们看成有理系数多项式，实系数多项式和复系数多项式，带余除法的结果都是一样的，即

。

下面我们介绍当是一次多项式时求商式与余式的简便方法

设=，那么余式,商式为，根据带余除法有

，

即

。

比较两边系数可得到

，

，   ，

，

于是可利用下面的表格算出的系数以及余式

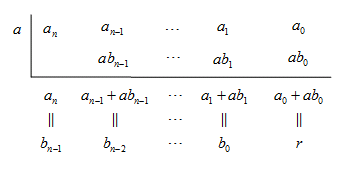
这种算法称为综合除法。

例2.3.1 用综合除法计算被除的商式和余式。

解 用综合除法列表如下

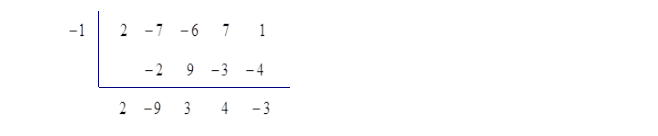
因此商式，余式

边学边练

1. 用除，求商式和余式

， 。

2. 用综合除法求一次多项式除所得的商式和余式

(1)， ；

3. 设有多项式,,且若，且，则。

4. 设为两个不相等的常数，证明多项式被除所得余式为。