讲三个问题：（1）整数的整除；（2）最大公因数；（3）整数集的唯一因子分解定理  

(1)整数的整除  

整数集由正整数，负整数及零构成。我们熟知，两个整数的和，差，积仍然是一个整数。但是两个整数相除（除数不为零）则不一定得整数。这一点可以说是整数集的一个特点。整除理论就产生于整数的上述特点。

整数集中有带余除法

定理2.1.1(带余除法） 设是整数集中的任意整数， 则存在唯一的一对整数使得   0＜。

证明:  存在性  考虑集合

若＞0，则 若＜0，则。因此非空，由最小数原理中存在一个最小数，设为。令，根据的定义，，且。若，且＞0，则，从而。即，于是，即。但＜与的取法矛盾。若，且＜0，则。于是，但＜与的选取矛盾。所以＜。存在性得证。

唯一性 若还有,使得

, ＜，

则得 ，  于是。

不妨设， 因为＜＜，

所以＜ ， 于是＜1。

由此可得即，从而。

定义2.1.1 设都是整数，如果存在整数，使得，则称整除记为，称为是的因数，称为的倍数，若不整除，记为。

定理2.1.2  设都是整数。

（1）, 当且仅当（此时称与是相伴的）；

（2）若则；

（3）若，则对任意整数有。

此定理的证明比较简单，读者作为练习。

（2）最大公因数

在整数环中有带余除法，从而可以证明任意两个整数都有最大公因数。

定义2.1.2 设是整数，若整数既是的因数，又是的因数，则称是与的公因数（或公因式）。设是与的一个公因数，如果与的每一个公因数都能整除，则称是与的一个最大公因数（或最大公因子）。

引理2.1.3  在整数环中，如果有等式

成立，则与的最大公因数和与的最大公因数相同。

定理2.1.4 任意给定两个整数，都存在它们的一个最大公因数，并且可表示成与的一个组合，即存在整数使得。

证明 如果，则就是与的一个最大公因数，并且

现在设，容易看出与的最大公因数是与的最大公因数，反之亦然，因此不妨设＞0，根据带余除法，有整数，使得

               ＜b

如果则用，有整数使得

             ＜

如果，再用去除，如此辗转相除下去，显然所得余数（正整数）不断减小，因此在有限次后，必然有余数为零。可设出最后一个不等于零的余数，就是与的一个最大公因数，并且它可以表示成与的一个组合。

上述定理证明过程是求两个整数最大公因数的辗转相除法。

从定义2.1.2可知，与的最大公因数在相伴的意义下（即相差一个正负号）是唯一的。对于不全为零的整数，，我们约定用表示正的那个最大公因数。

例 2.1.1 求 （3961，952）.

解：作如下辗转相除，列式如下：

39619524+153；

9521536+34；

153344+17；

34172.

由上得（3961，952）17.

定义2.1.3  设,如果，则称与互素。

显然，如果两个整数互素，那么它们除去以外没有其它公因数，反之亦然。

定理2.1.5  两个整数与互素的充分必要条件是有整数，使得。

证明： 必要性从定理2.1.4立即得出，充分性易证。

推论2.1.6  在整数环中，如果，并且，则。

完全类似地也可以定义多个整数的最大公因数。

（3）整数集唯一因子分解定理

定义2.1.4  一个大于1的整数，如果它的正因数只有1和它本身，就叫做素数，否则就叫做合数。

由定义立即得出

命题2.1.7  设为一个素数，为任一整数，则或者，或者。

命题2.1.8 设为一个素数，那么对于任意整数，由可以推出。

证明：用反证法。设，又，由命题2.1.7，得

于是有，从而，与定理的假设矛盾。

命题2.1.9 如果为素数，若，其中都为整数，则一定整除某个。

定理2.1.10（整数的唯一因子分解定理）任一大于1的整数能唯一地分解成有限个素数的乘积，所谓唯一性是说，如果有两个这样的分解式

则一定有，并且适当排列因子的次序后有

。

证明  先证存在性。用数学归纳法。当时，是素数，因此结论成立。

假设对小于且大于的一切整数，结论成立。考虑()，如果是素数，则结论成立；如果是合数，则有两个大于且小于的整数，使得。由归纳假设，与分别能分解成有限个素数乘积，从而能分解成有限个素数的乘积。由归纳法原理，存在性得证。

再证唯一性，对个数s用数学归纳法。当时，是素数，分解显然是唯一的.假设时结论成立，考虑因子个数为，即有

因为，由命题2.1.8,整除某个.不妨设。因为为素数，故有。于是有。由归纳假设必有，即. 适当排列因子的次序有 ,由归纳假设原理，唯一性得证。

由定理2.1.10知道，任一大于的整数能唯一写成

=

其中是不同的素数，是正整数，上式称为的标准分解式。

如果已知两个大于的整数的标准分解式

=，，

则,其中。

边学边练

1.证明：。

证明：若，则可得结论。否则有或。若有，则有

，所以 ，因此。若有，则有

，所以 ，于是有。

2.证明：若对任何均有，则。若对任何均有，则。

证明：（1）由任何均有，则有       ，，由的任意性，不仿取 ，有。

（2）由对任何均有，则有 ，由的任意性取 ，则有，则。

3.求 。

解：作如下辗转相除，得

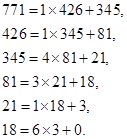
最后一个非零余数就是与 的最大公因数，即