当前位置:课程学习>>第二章 一元多项式理论概述>>学习内容>>文本学习>>知识点四
知识点四:最大公因式
如果多项式![]() 既是
既是![]() 的因式,又是
的因式,又是![]() 的因式,就称
的因式,就称![]() 为
为![]() 与
与![]() 的公因式。
的公因式。
定义2.4.1 设![]() ,如果多项式
,如果多项式![]() 具有以下两条性质:
具有以下两条性质:
(1) ![]() 是
是![]() 与
与![]() 的公因式;
的公因式;
(2)![]() 与
与![]() 的公因式都是
的公因式都是![]() 的因式,
的因式,
则称![]() 为
为![]() 与
与![]() 的一个最大公因式
的一个最大公因式
从定义立即得出,两个零多项式的最大公因式就是0;对于任意多项式![]() ,
,![]() 是
是![]() 与0的一个最大公因式.
与0的一个最大公因式.
对于![]() 中任意两个多项式,是否存在它们的最大公因式?如果存在,如何找出它们的最大公因式?进一步,它们的最大公因式是否唯一?本节将讨论这些问题。
中任意两个多项式,是否存在它们的最大公因式?如果存在,如何找出它们的最大公因式?进一步,它们的最大公因式是否唯一?本节将讨论这些问题。
引理2.4.1在![]() 内如果有以下等式:
内如果有以下等式:
![]() ,
,
那么![]() 和
和![]() 有相同的公因式,从而有相同的最大公因式集合。
有相同的公因式,从而有相同的最大公因式集合。
证明 设![]() 是
是![]() ,
,![]() 的一个公因式,则
的一个公因式,则![]() ,
,![]() ,则有
,则有
![]()
所以![]() 是
是![]() 与
与![]() 的公因式.反之,如果
的公因式.反之,如果![]() 是
是![]() ,
,![]() 的一个公因式,
的一个公因式,![]() ,
,![]() ,则有
,则有![]() .所以
.所以![]() 是
是![]() ,
,![]() 的公因式
的公因式
定理2.4.2 对于![]() 中任意两个多项式
中任意两个多项式![]() ,
,![]() ,在
,在![]() 中一定存在最大公因式,且
中一定存在最大公因式,且![]() 与
与![]() 的任意最大公因式
的任意最大公因式![]() 都可以表示成
都可以表示成![]() 和
和![]() 的一个组合,即有
的一个组合,即有![]() 中的多项式
中的多项式![]() ,
,![]() ,使得
,使得
![]() =
=![]()
![]() +
+![]()
![]() (2.4.1)
(2.4.1)
证明 如果![]() =0,则
=0,则![]() 就是
就是![]() 与
与![]() 的一个最大公因式,并且
的一个最大公因式,并且
![]()
现在设![]()
![]() ,根据带余除法,用
,根据带余除法,用![]() 去除
去除![]() 可得商式和余式
可得商式和余式![]() ,
,![]()
![]()
![]() ;如果
;如果![]() ,则用
,则用![]() 去除
去除![]() ,可得商式与余式
,可得商式与余式![]()
![]() ,
,![]()
![]()
![]() ;又如果
;又如果![]() ,再用
,再用![]() 去除
去除![]() ,可得到商式和余式
,可得到商式和余式![]() ,
,![]()
![]()
![]() ;如此辗转相除,所得余式的次数不断降低
;如此辗转相除,所得余式的次数不断降低
![]() >
>![]() >
>![]() >…
>…
因此在有限次后必然有余式等于0,不妨设![]() 是第一个等于0的余式,于是得到下列等式:
是第一个等于0的余式,于是得到下列等式:
![]() ,
,![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
… …
![]() ,
,![]()
… …
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
![]() ,0的一个最大公因式是
,0的一个最大公因式是![]() ,根据引理2.4.1,
,根据引理2.4.1,![]() 也是
也是![]() ,
,![]() 的一个最大公因式;依此反推上去,
的一个最大公因式;依此反推上去,![]() 就是
就是![]() ,
,![]() 的一个最大公因式.
的一个最大公因式.
由上面的倒数第二个等式,得
![]()
再由倒数第三式
![]()
代入上式可消去![]() ,得到
,得到
![]()
用同样的方法由下至上逐个地消去![]() ,…,
,…,![]() ,最终得到
,最终得到
![]()
其中![]() ,
,![]()
![]()
![]() .
.
由最大公因式的定义不难看出,如果![]() ,
,![]() 是
是![]() 与
与![]() 的两个最大公因式,那么一定有
的两个最大公因式,那么一定有![]() ,
,![]() 也就是说
也就是说![]() 与
与![]() 是相伴多项式,即
是相伴多项式,即![]() =
=![]() ,
,![]() 。因此两个多项式的最大公因式在可以相差一个非零常数倍的意义下是唯一确定的。此时,我们约定,用
。因此两个多项式的最大公因式在可以相差一个非零常数倍的意义下是唯一确定的。此时,我们约定,用![]() 表示首系数为
表示首系数为![]() 的那个最大公因式,当
的那个最大公因式,当![]() 时,规定
时,规定![]() 。
。
定理证明中用来求最大公因式的方法通常称为辗转相除法。
例2.4.1 设![]() ,
,
![]()
![]() ,
,
求![]() ,并求
,并求![]() ,
,![]() 使得
使得
![]()
![]()
![]()
![]() +
+![]() 。
。
解 用辗转相除法

用等式写出来,就是
![]()
![]()
![]()
![]()
![]() ,
,
因之 ![]() 。
。
而 ![]()
![]()
![]()
![]() ,
,
于是 ![]() 。
。
定义2.4.2 如果![]() 的最大公因式
的最大公因式![]() 则称
则称![]() 与
与![]() 互素。
互素。
显然,如果两个多项式互素,那么它们除去零次多项式外没有其它的公因式,反之亦然。
下面给出两个多项式互素的一个充分必要条件,它非常有用。
定理2.4.3 两个多项式![]() 互素的充分必要条件是存在
互素的充分必要条件是存在![]() ,
,![]()
![]()
![]() ,使得
,使得
![]() 。
。
证明 必要性是定理2.4.2的直接推论.现在证充分性,设有![]() ,使得
,使得
![]()
再设![]() , 从而
, 从而
![]() ,
,
因此 ![]() , 即
, 即![]() 互素。
互素。
推论2.4.4 如果![]() ,且
,且![]() ,则
,则![]() 。
。
证明 由![]() 互素,可知存在
互素,可知存在![]() ,
,![]() 使得
使得
![]() 。
。
等式两边乘以![]() ,得
,得
![]() 。
。
因为![]() ,所以
,所以![]() 整除等式左端,从而
整除等式左端,从而![]() 。
。
推论2.4.5 如果![]() ,
,![]() 且
且![]() ,那么
,那么![]() 。
。
证明 由![]() 有
有![]() 使
使![]() 。
。
又因为 ![]() 且
且![]() ,可得
,可得![]() ,从而存在
,从而存在![]() ,使得
,使得![]() ,故
,故![]() 。
。
所以![]() 。
。
注意:当![]() ,由于最大公因式是通过辗转相除法得到的,它的系数不会超出数域
,由于最大公因式是通过辗转相除法得到的,它的系数不会超出数域![]() 的范围,所以
的范围,所以![]() ,这就是说最大公因式与多项式的系数所在的域的扩张没有关系。
,这就是说最大公因式与多项式的系数所在的域的扩张没有关系。
![]()
![]()
边学边练
1.求![]() 与
与![]() 的最大公因式,并把
的最大公因式,并把![]() 表示成
表示成![]() 与
与![]() 的一个组合。
的一个组合。
(1)![]()
![]() ,
,![]() ;
;
(2)![]() ,
,![]() 。
。
答案 (1) ![]() ;
;
(2)![]() 。
。
2. 设![]() 是首一多项式,证明
是首一多项式,证明
![]()
![]() 。
。
答案 设![]() ,则存在
,则存在![]() ,使
,使![]() ,
,
所以![]() 。 又因
。 又因
![]()
![]() ,所以
,所以![]() 是
是![]() 和
和![]() 的一个最大公因式,又因
的一个最大公因式,又因![]() 都是首一多项式,故
都是首一多项式,故![]() 也是首一多项式,从而
也是首一多项式,从而
![]() . 又如
. 又如![]() ,则
,则![]() ,原等式仍然成立。
,原等式仍然成立。
3. 如果![]() 不全为零,证明
不全为零,证明
![]() 。
。
答案 因![]() 不全为零,则
不全为零,则![]() ,所以
,所以
![]()
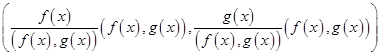
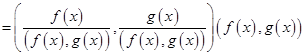
两边消去![]() ,得
,得![]() 。
。
4.设![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() 。
。
答案 由题设![]() 可得,又
可得,又![]()
![]() ,所以
,所以![]() ,又因
,又因
![]() 与
与![]() 的首项系数相同,故
的首项系数相同,故![]()
![]()
