中学数学中介绍了一些因式分解的方法，而且对多项式进行因式分解时，总是要求分到不能再分解的程度。但什么是不能再分呢？这是一个相对系数域情况而定的。

例如

在有理数域上就是不能再分了。但是在实数域上还可进一步分解为

在中,这个分解不能再分了,但在复数域上,又可进一步的分解为.

当然，这里不能再分了。由此可见，不可再分解是相对于系数域而言，下面给出

不可分的确切的数学定义。

定义2.5.1 设是次数的多项式。如果不能分解成两个次数比它低的上多项式的乘积，则称为数域上的不可约多项式。

如，是上的不可约多项式。但是上可约多项式，这是因为在中。这说明了，一个多项式是否不可约是依赖于系数域的。

由定义可以看出，次多项式一定是不可约的。而且不可约多项式没有真因式，即没有次数比它低的正次数因式。

命题2.5.1 设，且是上的不可约多项式，则或者。

证明：设，则，且。由于是不可约多项式，故一定是的相伴多项式。即，于是，即

定理2.5.2 设是不可约多项式，那么对于任意的多项式由一定能推出或。

证明：如果，结论成立。如果不整除，由命题2.5.1可知,据推论2.4.4有。

利用数学归纳法，这个定理可以推广为：如果不可约多项式整除一些多项式的乘积，即 ，那么一定整除这些多项式中某一个。

定理2.5.3 （因式分解及唯一性定理）数域上每一个次数的多项式都可以唯一地分解成数域上一些不可约多项式的乘积。所谓唯一性是说，如果有两个分解式

，

那么一定有，并且适当排列因式的次序后有，其中。

证明：先证存在性。对作数学归纳法。因为次多项式都是不可约的，所以时结论成立。现在假设结论对于小于次的多项式已经成立.考察次多项式。如果不可约，则结论是显然的。否则可以分解为两个次数小于的上的多项式的乘积：

，

于是都满足归纳法的假设，它们可以分解成上一些不可约多项式的乘积。把的分解式合起来就得到了的分解式，根据数学归纳法，结论对任意次数的多项式都成立。

再证唯一性。设可以分解成不可约多项式的乘积

，

如果还有另一个分解式

，

其中都是不可约多项式。于是

。              (2.5.1)

我们对于做归纳法。当，是不可约多项式，由定义必有

。

现在设唯一性结论对个不可约因式是正确的。由（2.5.1），因此，必整除其中某一个，不妨设。因为是不可约多项式，所以有

。                    （2.5.2）

在（2.5.1）式两边消去，就有

。

由归纳假设，有即.并且在适当排列次序后有

。

这样就证明了唯一性结论对个不可约因式是正确的，完成归纳法证明。

注意：因式分解定理虽然非常重要，但是它并没有给出一个具体的分解多项式的方法。事实上，在一般情况下，没有一个普遍适用的统一方法对多项式做因式分解。

在多项式的分解式中，所有的不可约因式都取成首一多项式，再把相同的因式合并成方幂，就可得到如下形式的分解式

，                    （2.5.3）

其中是的首项系数，是不同的首一不可约多项式，是正整数。这样的分解式称为标准分解式。

利用多项式的标准分解式可以得到两个多项式的最大公因式的标准分解式。为了叙述方便，对任何，约定

命题2.5.4 设，且有分解式

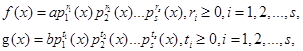
其中是不同的首一不可约多项式，则

  ，             （2.5.4）

其中。

证明：把（2.5.4）式右端的乘积记为。则为首一多项式，显然，因此。

作为的公因式，它的不可约因式只能是中的一部分，因此的分解式为

，

其中，从而。

由于，因此。这证明了，即。

例2.5.1 证明在有理数域上不可约。

证明：若在有理数域上可约，则它的标准分解式为  （2.5.5）

（2.5.5）式可以看作是在实数域上的不可约因式分解。另一方面在上有如下的不可约因式分解

。

由中分解的唯一性知

或，

由此推出  或，这与矛盾。因此在有理数域上不可约。

边学边练

1.证明.

答案  设其中，是两两互素的不可约首一多项式，且，则

。

2.设是次数大于零的多项式。证明：如果对于任何多项式，由可以推出或者。则是不可约多项式。

答案 若可约，则存在次数小于的非常数多项式使得，从而，但因不能整除，不能整除，与假设矛盾，因此不可约。

3.求下列多项式分别在复数域，实数域和有理数域上标准分解式

（1）  ； （2）。

答案 ⑴ 实数域：。

复数域： 。

有理数域：令，则，，由艾森斯坦因判别法知，在有理数域上不可约。

⑵ 实数域： 。

复数域： 。

有理数域：。