本节用代数方法定义多项式的导数，并用它研究一个多项式何时有重因式.

定义2.6.1 设，，且是不可约多项式，如果，，则称是的重因式，当，是单因式，＞1时是重因式，时，不是的因式。

显然，如果的标准分解式是

，

那么，分别是的重，重，…重因式。

因为没有一般的方法求出一个多项式的标准分解式，判别有没有重因式的问题需要另找方法，为此引入多项式导数的概念

定义2.6.2 对于中多项式

把中的多项式

称为的导数（或一阶导数），记为

类似地，的导数叫做的二阶导数，记为；的导数叫做的三阶导数，记为；依此类推，的阶导数记为。

虽然多项式的导数的概念来源于微积分，但是我们这里完全是形式地加以定义，没有用到极限与连续的概念，因此也与数域的选取无关。

通过定义直接验证多项式导数有下列性质：

，

，，

，

，。

命题2.6.1 如果不可约多项式是的重因式，则是导数的重因式，特别地，多项式的单因式不是它的导数的因式。

证明：因为是的重因式，所以存在使得

，。

求的导数，得

因为，并且是不可约的，所以。但是，所以不能整除上述等式右端括号里的和，因此是的重因式。

推论2.6.2 不可约多项式是的重因式的充分必要条件为是与的公因式.

证明 的重因式必定是的因式。反之，如果的不可约因式是单因式，它一定不是的因式。

推论2.6.3 多项式没有重因式的充分必要条件是

。

例2.6.1 判断有无重因式，如果有求出其重数。

解：利用辗转相除法：

。

因此与有公因式，且是的单因式，所以仅有一个二重因式。

推论2.6.4 设多项式有标准分解式

其中是互不相同的首一多项式，则

，

因此，

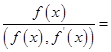
是与有相同不可约因式，而又不含重因式的多项式。

例2.6.2  求的标准分解式

解  ，

利用辗转相除法得

         ，

所以     。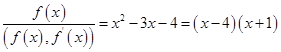

故与分别是的因式，直接验证是的单因式，而是的重因式。所以。

 

边学边练

 

1. 证明下列关于多项式的导数的公式

（1），

（2）。

答案 直接根据导数定义。

2. 判别下列有理系数多项式有无重因式

（1），

（2）。

答案 ⑴ 有，，是重因式。⑵ 无重因式。

1.判断多项式有无重因式。如果有，试求出重数。

答案  ，用辗转相除法，且是的二重因式。

2.写出多项式的标准分解式。

答案  。

3.试求多项式除以所得余式。

答案  设，则两边求导后得 ，以代入上两式，得

，故所求余式为