本章概述

一元多项式理论是高等代数的一个重要组成部分，他也是中学代数课程中最重要的部分。但是，中学是以多项式的具体运算为主，而这里是以多项式的理论为主。本章的重点是多项式因式分解理论和多项式的求根。在讲多项式因式分解理论时常常与整数的理论作对比，因为它们有许多相似之处。学习本章时，要正确掌握概念，学会严谨地推导和计算。

学习目标

1．了解一元多项式的定义，运算，次数及导数的概念与性质。

2. 理解多项式的整除，最大公因式，互素的概念与性质，特别是整除的性质，带余除法定理，最大公因式的存在表示定理，它们是多项式理论的基石。

3.理解多项式的因式分解理论，包括不可约多项式，因式分解，实系数与复系数多项式的因式分解，有理系数不可约多项式的判别等，并掌握它们的应用。

4.理解多项式的根，代数基本定理，根与系数的关系，有理系数多项式的有理根求法，并掌握它们的应用。

知识结构框图

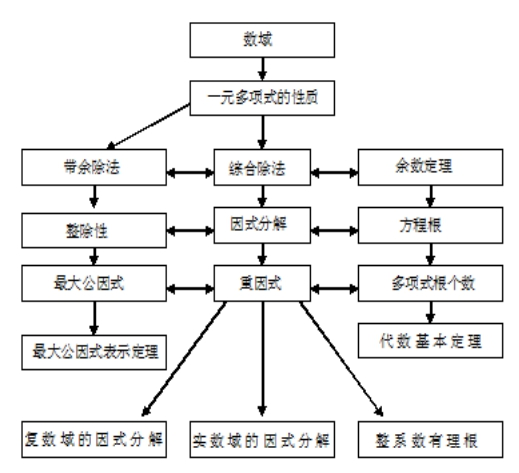
重点难点解析与学习建议

本章系统地给出了一元多项式的理论，它可分为四个方面：

（一）一般的理论。主要包括一元多项式的定义、运算，次数及导数的概念与性质。

（二）整除理论。包括整除，最大公因式，互素的概念与性质。

（三）因式分解理论。包括不可约多项式，因式分解，实系数与复系数多项式的因式分解，有理系数不可约多项式的判别等。

（四）根的理论。包括多项式函数，多项式的根，代数基本定理，根与系数的关系，有理系数多项式的有理根求法。三次及四次方程求根公式等。

一元多项式的内容十分丰富，重点是整除与因式分解理论，最基本的结论是带余除法，最大公因式的存在表示定理与因式分解唯一性定理。在学习过程中，如能牢牢把握这两个重点和三大定理，就能从整体上把握一元多项式理论。

难点是多项式不可约的概念，多项式的因式分解，有理多项式的不可约性的判定。

课前提问

1、数域的概念是如何定义的？你能给出几个具体的数域吗？

2、一元多项式是如何定义的？什么多项式是零次多项式？什么多项式是零多项式？一元多项式的次数是如何定义的？你能写出次数公式吗？

3、给出一元多项式整除的定义？给出多项式整除的基本性质？写出带余除法并能正确求出两个已知多项式的商式与余式？会用综合除法求商式与余式？

4、 多项式的最大公因式是如何定义的？如何求多项式的最大公因式？多项式的最大公因式的存在表示定理是什么？多项式的互素是如何定义的？有什么样的性质？

5、不可约多项式是如何定义的？不可约多项式的概念与多项式所在的数域是否有关？你能用具体的例子说明吗？

6、你能叙述多项式的因式分解唯一性定理吗？对这一定理你是如何理解的？

7、你能给出多项式的导数的定义吗？你能给出多项式的重因式的定义并举例说明吗？

8、如何理解多项式的根？多项式的根与多项式的一次因式有什么关系？

9、复数域上不可多项式是什么样？复数域上多项式的标准分解式是什么？代数基本定理如何？根与系数关系如何？

10、实数域上不可多项式是什么样？实数域上多项式的标准分解式是什么？实数域上多项式的复根有什么样的性质？

11、本原多项式是如何定义的？有什么样的重要性质？有理数域上有什么样的判别法用于判断有理数域上多项式不可约？

12、你认为这一章中的哪些实例或者练习题最有意思？哪些题目感觉较难，作为笔记的内容之一，试着总结一下.