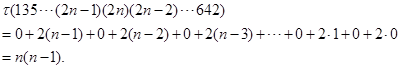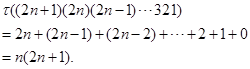作为定义级行列式的准备,我们先来讨论一下排列的性质.

定义1  由组成的一个有序数组称为一个级排列.

例如,是一个四级排列,是一个级排列.我们知道,级排列的总数是

.

我们记

.

读为“阶乘”.例如：,.随着的增大迅速地增大.例如：.

显然也是一个级排列,这个排列具有自然顺序,就是按递增顺序排起来的；其他的排列都或多或少地破坏自然顺序.

定义2  在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序,一个排列中逆序的总数就称为这个排列的逆序数.

例如中,,,,是逆序,的逆序数就是,而的逆序数是.

排列的逆序数记为.

定义3  逆序数为偶数的排列称为偶排列, 逆序数为奇数的排列称为奇排列.

例如,是偶排列；是奇排列；的逆序数是零,因之是偶排列.

应该指出,我们同样可以考虑由任意个不同的自然数所组成的排列,一般也称为级排列.对这样一般的级排列,同样可以定义上面这些概念.

把一个排列中某两个数的位置互换,而其余的数不动,就得到另一个排列.这样一个变换称为一个对换.例如,经过对换,排列就变成,排列就变成了.显然,如果连续施行两次相同的对换,那么排列就还原了.由此得知,一个对换把全部级排列两两配对,使每两个配成对的级排列在这个对换下互变.

关于排列的奇偶性,我们有下面的基本事实.

定理1  对换改变排列的奇偶性.

这就是说,经过一次对换,奇排列变成偶排列,偶排列变成奇排列.

证明  先看一个特殊的情形,即对换的两个数在排列中是相邻的情形.排列

                       

经过对换变成

                       

这里“”表示那些不动的数.显然,在排列中与其他的数构成逆序,则在排列中仍然构成逆序；如不构成逆序则在中也不构成逆序；不同的只是的次序.如果原来组成逆序,那么经过对换,逆序数就减少一个；如果原来不组成逆序,那么经过对换,逆序数就增加一个.不论增加还是减少,排列的逆序数的奇偶性总是变了.因此,在这个特殊的情形,定理是对的.

再看一般的情形,设排列为

                 

,                         

经过对换,排列变成

.                         

不难看出,这样一个对换可以通过一系列的相邻数的对换来实现,从出发,把与对换,再与对换…,也就是说,把一位一位地向左移动.经过次相邻位置的对换,排列就变成

                       

从出发,再把一位一位地向右移动,经过次相邻位置的对换,排列就变成了排列.因之,对换可以通过次相邻位置的对换来实现.是奇数、相邻位置的对换改变排列的奇偶性.显然,奇数次这样的对换的最终结果还是改变奇偶性.

根据定理1,可以证明以下重要结论.

推论  在全部级排列中奇、偶排列的个数相等,各有个.

证明  假设在全部级排列中共有个奇排列,个偶排列.

将个奇排列中的前两个数字对换,得到个不同的偶排列,因此.同样可证,于是,即奇、偶排列的总数相等,各有个.

定理2  任意一个级排列与排列都可以经过一系列对换互变,并且所作对换的个数与这个排列有相同的奇偶性.

证明  我们对排列的级数作数学归纳法,来证明任意一个级排列都可以经过一系列对换变成.

级排列只有一个,结论显然成立.

假设结论对级排列已经成立,现在来证对级排列的情形结论也成立.

设是一个级排列,如果,那么根据归纳法假设,级排列可以经过一系列对换变成,于是这一系列对换也就把变成.这就归结成上面的情形,因此结论普遍成立.

相仿地,也可以用一系列对换变成,因为是偶排列,所以根据定理1,所作对换的个数与排列有相同的奇偶性.

边学边练

1.决定以下排列的逆序数，并确定排列的奇偶性

（1）  ； （2）

2.选择使

（1）成偶排列 ；        （2）       成奇排列。

3.写出把排列 变成排列  的那些对换。

4.求下列排列的逆序数：

（1） ；（2）   .