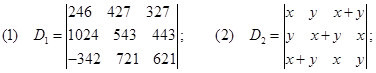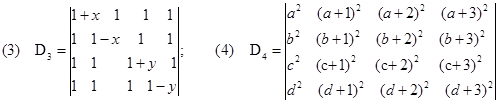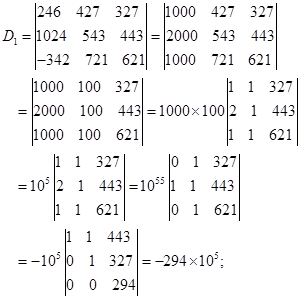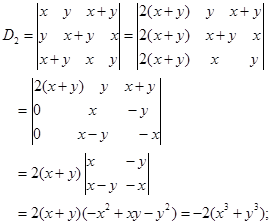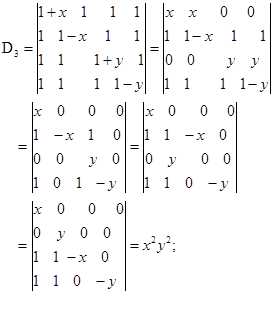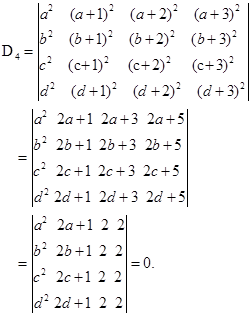当前位置:课程学习>>第三章 行列式>>学习内容>>视频课堂>>知识点五
知识点五:列式的计算
下面我们利用行列式的性质给出一个计算行列式的方法.
§3我们看到,一个上三角形行列式
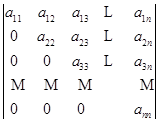
就等于它主对角线上元素的乘积
![]() .
.
这个计算是很简单的.下面我们想办法把任意的![]() 级行列式化为上三角形行列式来计算.
级行列式化为上三角形行列式来计算.
为了便于叙述并考虑到以后的应用,我们引进矩阵及矩阵的初等行变换的概念.
定义5 由![]() 个数排成的
个数排成的![]() 行(横的)
行(横的)![]() 列(纵的)的表
列(纵的)的表
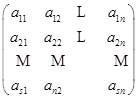
![]()
称为一个![]() 矩阵.
矩阵.
例如
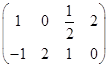
是一个![]() 矩阵,
矩阵,
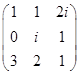
是一个![]() 矩阵.
矩阵.
数![]() ,
,![]() ,称为矩阵
,称为矩阵![]() 的元素,
的元素,![]() 称为元素
称为元素![]() 的行指标,
的行指标,![]() 称为列指标.当一个矩阵的元素全是某一数域
称为列指标.当一个矩阵的元素全是某一数域![]() 中的数时,它就称为这一数域
中的数时,它就称为这一数域![]() 上的矩阵,第二个是复数域上的矩阵.
上的矩阵,第二个是复数域上的矩阵.
![]() 矩阵也称为
矩阵也称为![]() 级方阵.一个
级方阵.一个![]() 级方阵
级方阵
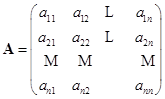
定义一个![]() 级行列式
级行列式
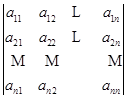
称为矩阵![]() 的行列式,记作
的行列式,记作![]() .
.
下面来定义矩阵的初等行变换.
定义6 所谓数域![]() 上矩阵的初等行变换是指下列三种变换:
上矩阵的初等行变换是指下列三种变换:
1)以![]() 中一个非零的数乘矩阵的某一行;
中一个非零的数乘矩阵的某一行;
2)把矩阵的某一行的![]() 倍加到另一行,这里
倍加到另一行,这里![]() 是
是![]() 中任意一个数;
中任意一个数;
3)互换矩阵中两行中的位置.
一般来说,一个矩阵经过初等行变换后就变成了另一个矩阵.譬如说,把矩阵
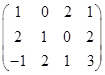
第一行的![]() 倍加到第二行,就得到矩阵
倍加到第二行,就得到矩阵
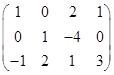
当矩阵![]() 经过初等行变换变成矩阵
经过初等行变换变成矩阵![]() 时,我们写成
时,我们写成
![]()
![]()
![]()
我们称形式如
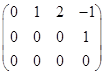 ,
,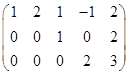 ,
,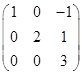
的矩阵为阶梯型矩阵.它们的任一行从第一个元素起至该行的第一个非零元素所在的下方全为零;如该行全为零,则它的下面的行也全为零.
可以证明,任意一个矩阵经过一系列初等行变换总能变成阶梯型矩阵.
事实上,设
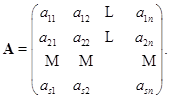
我们看第一列元素![]() ,
,![]() ,
,![]() ,
,![]() ,只要其中有一个不为零,用初等行变换3),总能使第一列的第一个元素不为零,然后从第二行开始,每一行都加上第一行的一个适当的倍数,于是第一列除去第一个元素外就全是零了.这就是说,经过一系列初等行变换后
,只要其中有一个不为零,用初等行变换3),总能使第一列的第一个元素不为零,然后从第二行开始,每一行都加上第一行的一个适当的倍数,于是第一列除去第一个元素外就全是零了.这就是说,经过一系列初等行变换后
![]()
![]()
![]()
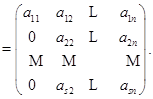
对于![]() 中右下角的一块
中右下角的一块
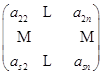
再重复以上的做法.如此作下去直到变成阶梯型为止.如果原来矩阵![]() 中第一列的元素全为零,那么就依次考虑它的第二列的元素,等等.例如,
中第一列的元素全为零,那么就依次考虑它的第二列的元素,等等.例如,
设
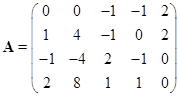 .
.
![]()
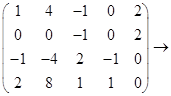
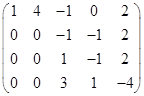
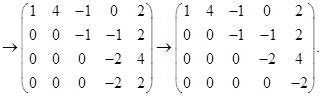
这样就把![]() 变成了一个阶梯型矩阵.
变成了一个阶梯型矩阵.
现在回过来讨论行列式的计算问题.一个![]() 级行列式可看成是由一个
级行列式可看成是由一个![]() 级方阵
级方阵![]() 决定的,对于矩阵可以作初等行变换,而行列式的性质2,6,7正是说明了方阵的初等行变换对于行列式的值的影响.每个方阵
决定的,对于矩阵可以作初等行变换,而行列式的性质2,6,7正是说明了方阵的初等行变换对于行列式的值的影响.每个方阵![]() 总可以经过一系列的初等行变换变成阶梯型方阵
总可以经过一系列的初等行变换变成阶梯型方阵![]() .由行列式性质2,6,7,对方阵每作一次初等行变换,相应地,行列式或者不变,或者差一非零的倍数,也就是
.由行列式性质2,6,7,对方阵每作一次初等行变换,相应地,行列式或者不变,或者差一非零的倍数,也就是
![]() ,
,![]() .
.
显然,阶梯形方阵的行列式都是上三角形的,因此![]() 是容易计算的.
是容易计算的.
例 计算
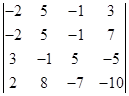 .
.
解
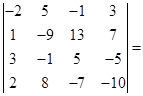
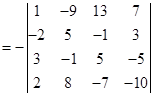
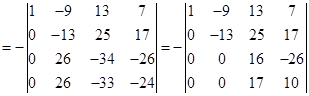
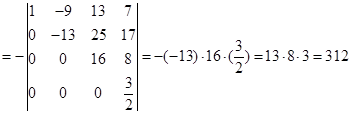
这里,第一步是互换第![]() 两行,以下都是把第一行的倍数加到另一行。不难算出,用这个方法计算一个
两行,以下都是把第一行的倍数加到另一行。不难算出,用这个方法计算一个![]() 级数字行列式只需要做
级数字行列式只需要做![]() 次乘法和除法.特别当
次乘法和除法.特别当![]() 比较大的时候,这个方法的优越性就更加明显了.同时还应该看到,这个方法完全是机械的,因而可以用电子计算机按这个方法来计算行列式的计算.
比较大的时候,这个方法的优越性就更加明显了.同时还应该看到,这个方法完全是机械的,因而可以用电子计算机按这个方法来计算行列式的计算.
最后我们指出,对于矩阵,我们同样地可以定义初等列变换,即
1)以数域![]() 中一非零数乘矩阵的某一列;
中一非零数乘矩阵的某一列;
2)把矩阵的某一列的![]() 倍加到另一列,这里
倍加到另一列,这里![]() 是
是![]() 中任意一个数;
中任意一个数;
3)互换矩阵中两列的位置.
为了计算行列式,我们也可以对矩阵进行初等列变换,有时候,同时用初等行变换和初等列变换,行列式的计算可以更简单些.
矩阵的初等行变换与初等列变换统称为初等变换.
边学边练
计算下列行列式