解方程是代数中一个基本的问题,特别是在中学所学代数中,解方程占有重要的地位.因此这个问题是读者所熟悉的.譬如说,如果我们知道了一段导线的电阻,它的两端的电位差,那么通过这段导线的电流长度就可以由关系式

求出来.这就是通常所谓解一元二次方程的问题.在中学所学代数中,我们解过一元、二元、三元以至四元一次方程组.在这一章和下一章主要地就是讨论一般的多元一次方程组,即线性方程组.这一章是引进行列式来解线性方程组,而下一章则在更一般的情况下来讨论一般的多元一次方程作用,即线性方程组.这一章是引进行列式来解决线性方程组,而在下一章则在更一般的情况下来讨论解线性方程组的问题.

线性方程组的理论在数学中是最基本的也是重要的内容.

对于二元线性方程组

,,

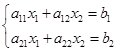当时,此方程组有唯一解,即

,.

我们称为二级行列式,用符号表示为

.

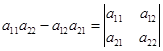于是上述解可以用二级行列式叙述为：

当二级行列式

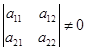
时,该方程组有唯一解,即

,.

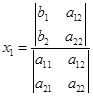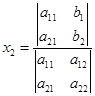对于三元线性方程组有相仿的结论. 设有三元方程组

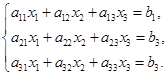
称代数式为三级行列式,用符号表示为：

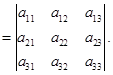
我们有：当三级行列式

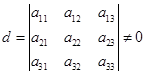
时,上述三元线性方程组有唯一解.解为

,,,

其中

   ，，.

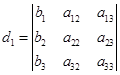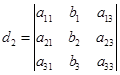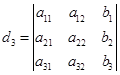在这一章我们要把这个结果推广到元线性方程组

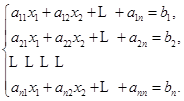
的情形. 为此,我们首先要给出级行列式的定义并讨论它的性质,这就是本章的主要内容.