我们现在来给出级行列式的定义.从这一节开始,我们总是取一固定的数域作为基础,所谈到的数都是指这个数域中的数,所考虑的行列式也都是数域上的行列式,以后就不重复说明了.

在给出级行列式的定义之前,先来看一下二级和三级行列式的定义.我们有

                 

            

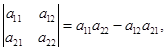
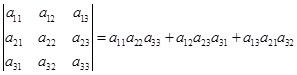
从二级和三级行列式的定义中可以看出,它们都是一些乘积的代数和,而每一项乘积都是由行列式中位于不同的行和不同的列的元素构成的,并且展开式恰恰就是由所有这种可能的乘积组成.在时,由不同行不同列的元素构成的乘积只有与这两项,在时也不难看出只有中的项.这是二级和三级行列式的特征的一个方面.另一方面,每一项乘积都带有符号.这符号是按什么原则决定的呢？在三级行列式的展开式中,项的一般形式可以写成

,                             

其中是的一个排列.可以看出,当是偶排列时,对应的项在中带有正号,当是奇排列时带有负号.二级行列式显然也符合这个原则.

上面对二级和三级行列式的分析对于我们理解一般的定义是有帮助的.下面就来给出级行列式的定义.

 

定义4  级行列式

                         

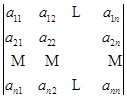
等于所有取自不同行不同列的个元素的乘积

                             

的代数和,这里是的一个排列,每一项都按下列规则带有符号：当是偶排列时,带有正号,当是奇排列时,带有负号,这一定义可写成

,

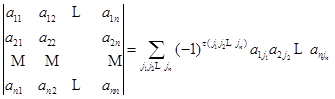这里表示对所有的级排列求和.

定义表明,为了计算级行列式,首先作所有可能由位于不同行不同列元素构成的乘积.把构成这些成绩的元素按行指标排成自然顺序,然后由列指标所成的排列的奇偶性来决定这一项的符号.

由定义立即看出,级行列式是由项组成的.

下面来看几个例子

例1  计算行列式

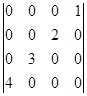
这是一个四级行列式,在展开式中应该有项.但是由于出现很多的零,所以不等于零的项数就大大减少了.我们具体地来看一下.展开式中项的一般形式是

.

显然,如果,那么,从而这个项就等于零.因此只需考虑那些项；同理,只需考虑,,这些列指标的项.这就是说,行列式中不为零的项只有这一项,而,这一项前面的符号应该是正的.所以

.

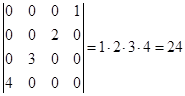例2  计算上三角行列式

                        

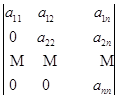
我们先来看一下,形如(5)式的项有哪一些不为零,然后再来决定它们的符号.项的一般形式为

,

在行列式中第行的元素除去以外全为零,因此,只要考虑的那些项.在第行中,除去外,其余的项全为零,因之只有这两种可能.由于,所以就不能等于了,从而.这样逐步推上去,不难看出,在展开式中,除去

这一项外,其余的项全是.而这一项的列指标所成的排列是一个偶排列,所以这一项带正号.于是

.                   

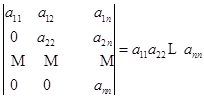换句话说,这个行列式就等于主对角线(从左上角到右下角这条对角线)上元素的乘积.作为的特殊情形,有

,                  

.                           

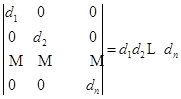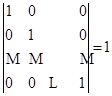主对角线以外的元素全为零的行列式称为对角形行列式.说明了对角形行列式的值等于主对角线上元素的乘积.

容易看出,当行列式的元素全是数域中的数时,它的值也是数域中的一个数.

在行列式的定义中,为了决定每一项的正负号,我们把个元素按行列指标排起来.事实上,数的乘法是交换的,因而这个元素的次序是可以任意写的,一般地,级行列式中的项可以写成

,                               

其中,是两个级排列.利用排列的性质,不难证明, 的符号等于

.                             

事实上,为了根据定义来决定的符号,就要把这个元素重新排一下使得它们的行指标成自然顺序,也就是排成

.                         

于是它的符号是

.                           

现在来证明, 与是一致的.我们知道,由变到可以经过一系列元素的对换来实现.每作一次对换,元素的行指标与列指标所成的排列与就都同时作一次对换,也就是与同时改变奇偶性,因而他们的和与的奇偶性不改变.也就是说,对作一次元素的对换不改变的值.因此,在一系列对换之后有

.

例如,是级行列式中一项,,,于是它的符号应为.如按行指标排列起来,就是,因而它的符号也是.

按来决定行列式中每一项的符号的好处在于,行指标与列指标的地位是对称的,因而为了决定每一项的符号,我们同样可以把每一项按列指标排起来,于是定义又可写成

.                   

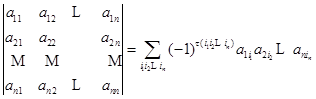由此即得行列式的下列性质：

性质1  行列互换,行列式不变.即

.                

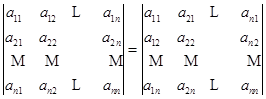事实上,元素在的右端位于第行第列,这就是说,是它的列指标,是它的行指标.因之,把右端按展开就等于

,

它正是左端按的展开式.

性质1表明,在行列式中行与列的地位是对称的,因之凡是有关行的性质,对列也同样成立.例如,由即得下三角形的行列式

.                

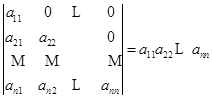下面我们所谈的行列式的性质大多是对行来说的,对于列也有相同的性质,就不重复了.

边学边练

1.确定下列行列式的项前面所带符号：

（1） ； （2）

解：（1），所以前面应取正号；

（2），所以该项取正号。

2.下列各项是否是五级行列式的项（包括符号）？

（1）；        （2）。

解：（1）不是的排列，所以该项不是五级行列式的项。

（2）都是的排列，所以该项是五级行列式的项。又因为，

，所以该项所带符号为正。

3．写出四级行列式中所有带负号且包含因子 项。

解：四级行列式中包含因子 项为，其中是的排列。的排列共有六个，所以这样的项共有六个。把的每个排列代入使这些项具体化。由于中是仅有的奇排列，所以四级行列式中带负号且含有因子的项是

4.在级行列式中，主对角线上各元素的乘积和次对角线上各元素的乘积分别应取什么符号？

解：主对角线上各元素的乘积为，的逆序数为，所以这项应取正号。

次对角线上各元素的乘积为， ，当，这项为负号，当

，这项取正号。

5.按定义计算下列行列式：

 ；

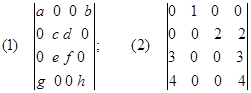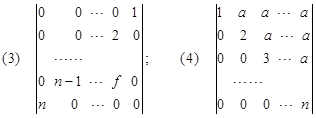
解：

（1）；

（2）

（3）；

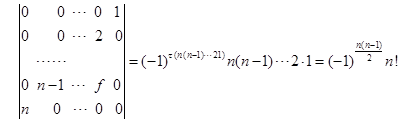（4）