行列式的计算是一个重要的问题,也是一个麻烦的问题.级行列式一共有项,计算它就需要做个乘法.当较大时,是一个相当大的数字.直接从定义来计算行列式几乎是不太可能的事.因此我们有必要进一步讨论行列式的性质.利用这些性质可以简化行列式的计算.

在行列式的定义中,虽然每一项是个元素的乘积,但是由于这个元素是取自不同的行与列,所以对于某一确定的行中个元素(譬如,,,)来说,每一项都含有其中的一个且只含有其中的一个元素.因之,级行列式的项可以分成组,第一组的项都含有,第二组的项都含有等等.再分别把行的元素提出来,就有

 ,               

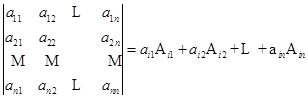其中代表那些含有的项在提出公因子之后的代数和.至于究竟是哪一些项的和我们暂且不管,到§6再来讨论.从以上讨论可以知道,中不再含有第行的元素,也就是全与行列式中第行的元素无关.由此即得

性质2

.

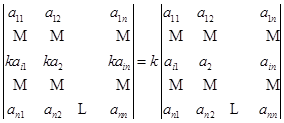这就是说,一行的公因子可以提出去,或者说以一数乘行列式的一行就相当于用这个数乘此行列式.

事实上,由

.

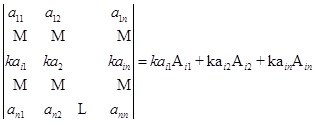
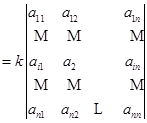令,就有,如果行列式中一行为零,那么行列式为零.

性质3

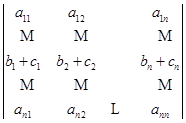
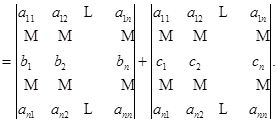
也就是说,如果某一行是两组数的和,那么这个行列式就等于两个行列式的和,而这两个行列式除这一行以外全与原来行列式的对应的行一样.

事实上,设这一行是第行,于是

.

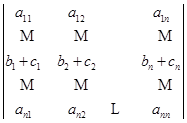
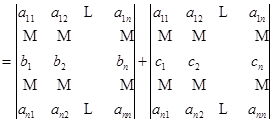性质3显然可以推广到某一行为多组数的和的情形,读者可以自己写出来.

再根据排列的性质,我们有：

性质4  如果行列式中有两行相同,那么行列式为零.所谓两行相同就是说两行的对应元素都相等.

证明  设行列式

               

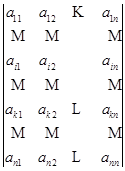
中第行与第行相同,即

,.                    

为了证明为零,只需证明的右端所出现的项全能两两相消就行了.事实上,与项

同时出现的还有

.

比较这两项,由有,

也就是说,这两项有相同的数值.但是排列

与

相差一个对换,因而有相反的奇偶性,所以这两项的符号相反.易知,全部级排列可以按上述形式两两配对,因之,在的右端,对于每一项都有一数值相同但符号相反的项与之成对出现,从而行列式 为零.

由这三个性质不难推得行列式的其他性质.

性质5  如果行列式中两行成比例,那么行列式为零.

证明

,

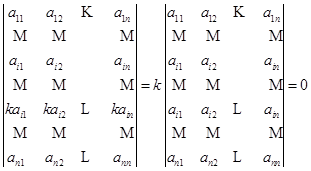这里第一步是根据性质2,第二步是根据性质4.

性质6  把一行的倍数加到另一行,行列式不变.

设

 

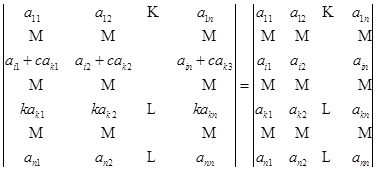
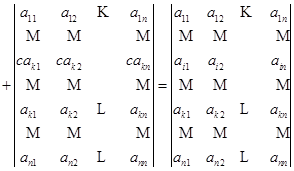
这里,第一步是根据性质3,第二步是根据性质5.

根据性质6即得

性质7  对换行列式中两行的位置,行列式反号.

证明

.

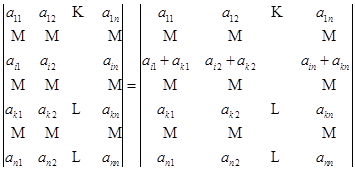
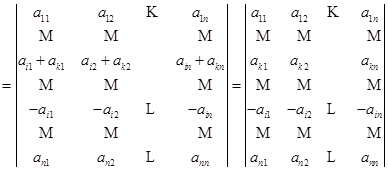
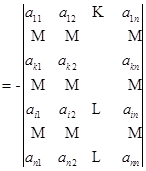这里,第一步是把第行加到第行,第二步是把第行的倍加到第行,第三步是把第行加到第行,最后再把第行的公因子提出.

作为行列式的性质的应用,我们来看下面两个例子.

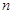1. 计算级行列式

.

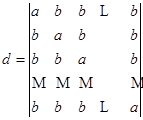这个行列式的特点是每一行有一个元素是,其余个元素是.根据性质6,把第二列加到第一列,行列式不变,再把第三列加到第一列,行列式也不变……直到第列也加到第一列,即得

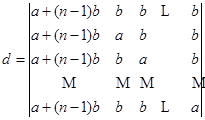
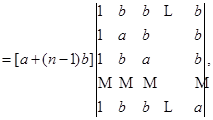
把第二行到第行都分别加上第一行的倍,就有

.

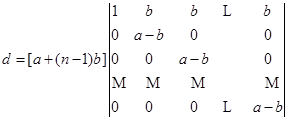这是一个上三角形的行列式,根据§3例2,得

.

1. 一个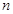级行列式,假设它的元素满足

,.

我们来证明,当为奇数时,此行列式为零.

由立即推知,,.

因此,此行列式明显地写出来就是

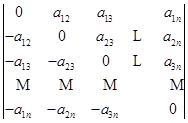
由性质1,2有

,

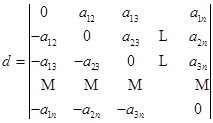
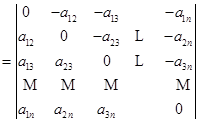
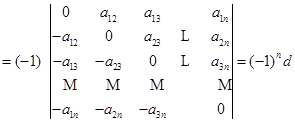当为奇数时,得,因而.

边学边练

1.计算下列行列式

 ；

 

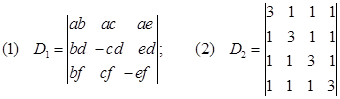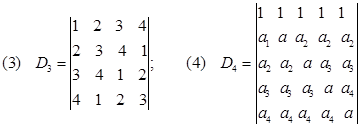
解：

（1）

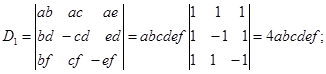
（2）

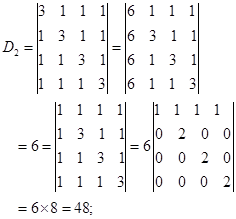
（3）

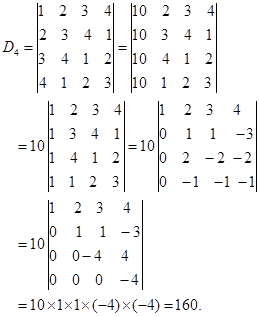
（4）

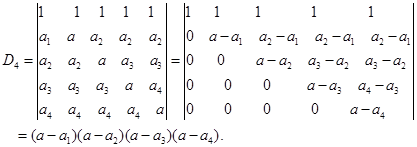
2.证明下列等式：

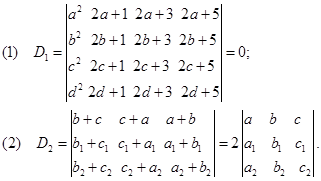
证明：（1）

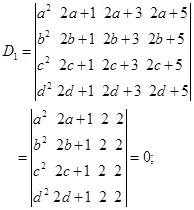
（2）