当前位置:课程学习>>第三章 行列式>>学习内容>>文本学习>>知识点六
知识点六:行列式按一行(列)展开
在§4我们看到,对于![]() 级行列式,有
级行列式,有
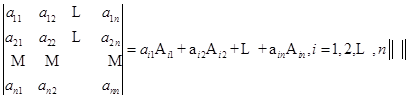
![]()
现在就来研究这些![]() ,
,![]() ,究竟是什么.
,究竟是什么.
我们知道,三级行列式可以通过二级行列式表示:
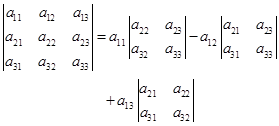
![]()
与此相仿![]() 也是一些带有正、负号的
也是一些带有正、负号的![]() 级行列式.为了说明这一点,我们引入
级行列式.为了说明这一点,我们引入
定义7 在行列式
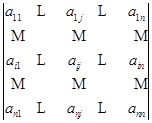
中划去元素![]() 所在的第
所在的第![]() 行与第
行与第![]() 列,剩下的
列,剩下的![]() 个元素按原来的排法构成一个
个元素按原来的排法构成一个![]() 级的行列式
级的行列式
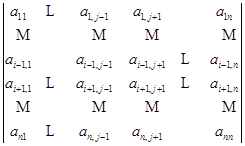
![]()
称为元素![]() 的余子式,记为
的余子式,记为![]() .
.
按这个定义,![]() 可以改写为
可以改写为
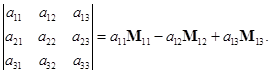
下面就来证明
![]() .
. ![]()
为此,我们先由行列式的定义证明![]() 级行列式与
级行列式与![]() 级行列式的下面这个关系,
级行列式的下面这个关系,
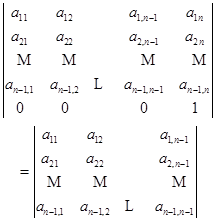
![]()
事实上,![]() 式左端行列式的展开式
式左端行列式的展开式
![]()
中只有![]() 的项才可能不为零,而
的项才可能不为零,而![]() ,因之左端为
,因之左端为
![]() .
.
显然![]() 是
是![]() 的排列,且
的排列,且
![]() .
.
这就证明了![]() .
.
为了证明![]() ,在
,在![]() 中令
中令
![]() ,
,![]() ,
,
即得
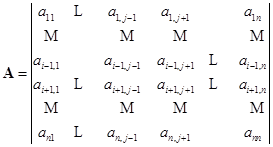
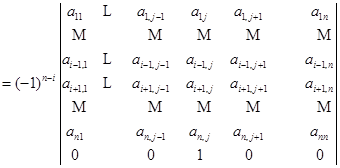
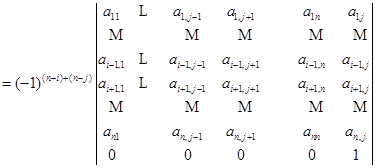
![]()
这里,第一步是依次地把第![]() 行与它下边的第一行对换,直到把它换到第
行与它下边的第一行对换,直到把它换到第![]() 行为止,这样一共换了
行为止,这样一共换了![]() 次,因之行列式差一个符号
次,因之行列式差一个符号![]() ;第二步是同样地把第
;第二步是同样地把第![]() 列换到第
列换到第![]() 列;再利用
列;再利用![]() 与显然的关系
与显然的关系![]() 即得
即得![]() .
.
定义8 上面所谈到的![]() 称为元素
称为元素![]() 的代数余子式.
的代数余子式.
这样,公式![]() 就是说,行列式等于某一行的元素分别与它们代数余子式的乘积之和,在
就是说,行列式等于某一行的元素分别与它们代数余子式的乘积之和,在![]() 中,如果令第
中,如果令第![]() 行的元素等于另外一行,譬如说,第
行的元素等于另外一行,譬如说,第![]() 行的元素,也就是
行的元素,也就是
![]() ,
,![]() ,
,![]() .
.
于是
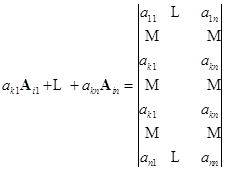 第
第![]() 行
行
右端的行列式含有两个相同的行,应该为零,这就是说,在行列式中,一行的元素与另一行相应元素的代数余子式的乘积之和为零.
基于行列式中行与列的对称性,在以上的公式和讨论中把行换成列也一样.综上所述,即得
定理3 设
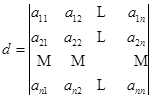 ,
,
![]() 表示元素
表示元素![]() 的代数余子式,则下列公式成立:
的代数余子式,则下列公式成立:
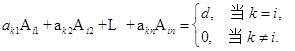
![]()
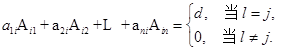
![]()
用连加号简写为
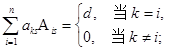
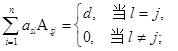
在![]() 时,公式
时,公式![]() 有明显的几何意义,如果把行列式的行看作向量在直角坐标系下的坐标,即设
有明显的几何意义,如果把行列式的行看作向量在直角坐标系下的坐标,即设
![]() ,
,![]() ,
,![]() ,
,
那么
![]()
于是
![]() ,
,
![]() ,
,
![]() .
.
在计算数字行列式时,直接应用展开式![]() 和
和![]() 不一定能简化计算,因为把一个
不一定能简化计算,因为把一个![]() 级行列式的计算换成
级行列式的计算换成![]() 个
个![]() 级行列式的计算并不减少计算量,只是在行列式中某一行或某一列含有较多的零时,应用公式
级行列式的计算并不减少计算量,只是在行列式中某一行或某一列含有较多的零时,应用公式![]() 或
或![]() 才有意义.但这两个公式在理论上是重要的.
才有意义.但这两个公式在理论上是重要的.
- 行列式
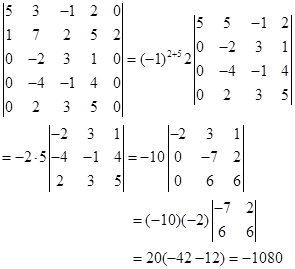
这里第一步是按![]() 列展开,然后再按第一列展开,这样就归结到一个三级行列式的计算.
列展开,然后再按第一列展开,这样就归结到一个三级行列式的计算.
- 行列式
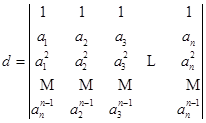
![]()
称为![]() 级的范德蒙德(Vandermonde)行列式.我们来证明,对任意的
级的范德蒙德(Vandermonde)行列式.我们来证明,对任意的![]() ,
,![]() 级范德蒙德行列式等于
级范德蒙德行列式等于![]() 这
这![]() 个数的所有可能的差
个数的所有可能的差![]() 的乘积.
的乘积.
我们对![]() 作归纳法.
作归纳法.
当![]() 时,
时,
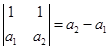
结果是对的。设对于![]() 级的范德蒙德行列式结论成立,现在来看
级的范德蒙德行列式结论成立,现在来看![]() 级的情形.
级的情形.
在![]() 中,第
中,第![]() 行减去第
行减去第![]() 的
的![]() 倍,第
倍,第![]() 行减去第
行减去第![]() 行的
行的![]() 倍,也就是由下而上地从每一行减去它上一行的
倍,也就是由下而上地从每一行减去它上一行的![]() 倍,有
倍,有
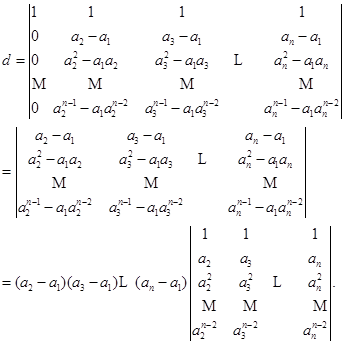
后面这行列式是一个![]() 级的范德蒙德行列式,根据归纳法假设,它等于所有可能差
级的范德蒙德行列式,根据归纳法假设,它等于所有可能差![]() 的乘积;而包含
的乘积;而包含![]() 的差全在前面出现了.因之,结论对
的差全在前面出现了.因之,结论对![]() 级范德蒙德行列式也成立.根据数学归纳法,完成了证明.
级范德蒙德行列式也成立.根据数学归纳法,完成了证明.
用连乘号,这个结果可以简写为
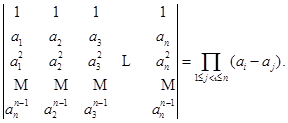
由这个结果立即得出,范德蒙德行列式为零的充分必要条件是![]() ,
,![]() ,
,![]() ,
,![]() ,这
,这![]() 个数中至少有两个相等.
个数中至少有两个相等.
例1 证明:
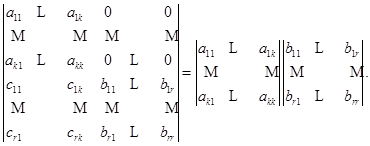
我们对![]() 用数学归纳法.
用数学归纳法.
当![]() 时,
时,![]() 的左端为
的左端为
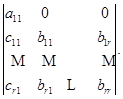
按第一行展开,就得到所要的结论.
假设![]() 对
对![]() ,即左端行列式的左上角是
,即左端行列式的左上角是![]() 级时已经成立, 现在来看
级时已经成立, 现在来看![]() 的情形,按第一行展开,有
的情形,按第一行展开,有
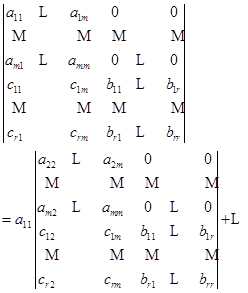
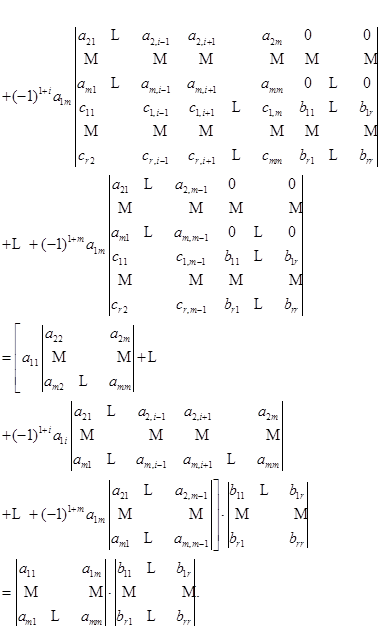
这里第二个等号是用了数学归纳法假定,最后一步是根据按一行展开的公式.
根据归纳法原理,![]() 式普遍成立.
式普遍成立.
边学边练
1.求下列行列式的代数余子式
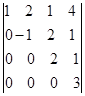
解:
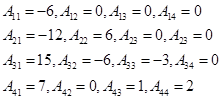
2. 求下列行列式
(1)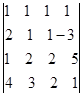 ; (2)
; (2)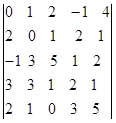
解:(1)1 ;(2) -483
3. 计算![]() 阶行列式
阶行列式
(1)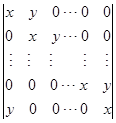 ; (2)
; (2)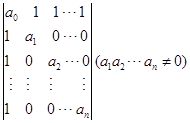
解:(1) ![]() ;(2)
;(2) ![]()
4.已知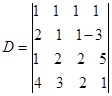 ,求
,求![]() 的值。
的值。
解: ![]()
