本章概述

行列式的概念是在解线性方程组的过程中产生的。中学给出过二阶，三阶行列式的概念，我们把它推广到 阶，并系统地介绍它的运算性质及在解线性方程组中的应用。 行列式的概念简单，但计算行列式的技巧及行列式的应用比较灵活，注意熟练掌握。

学习目标

1.本章重点是行列式性质与行列式的计算，难点是n阶行列式的定义。

2.掌握行列式定义，会利用定义计算行列式。

3.明确行列式各条性质

4.会利用行列式的各条性质计算较复杂的行列式。

5.应用行列式解方程组。

知识结构框图

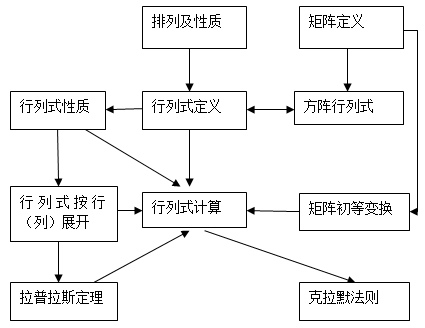
重点难点解析与学习建议

本章系统地给出了n阶行列式的理论及在线性方程组求解的应用。

会应用行列式的性质和按行（列）展开法则计算行列式是本章的重点。要求熟练正确地计算低阶行列式，也要会计算一些特殊形式的n阶行列式。

掌握行列式的计算方法和技巧是本章的难点。除了利用行列式的性质化为三角行列式和按行（列）展开法则使行列式降阶这些常用手法外，要根据行列式不同特点采用特殊方法，如递推法，数学归纳法，加边法以及利用范德蒙德行列式的结论等等。

作为行列式在解线性方程组中的应用，得出了克拉默法则。可是它只能应用于方程个数与变量个数相等的情形，而且还要系数行列式不等于零，一般情形，需要用其它方法求解。

课前提问

1、你能给出排列的定义吗？

2、你能给出排列的逆序数的定义，并举例说明吗？

3、你能给出奇偶排列的定义，并举例说明吗？

4、 给出二阶，三阶行列式及n阶行列式的定义。

5、不可约多项式是如何定义的？不可约多项式的概念与多项式所在的数域是否有关？你能用具体的例子说明吗？

6、行列式的行或列互换，其值有何变化？

7、行列式的某一行（或某一列）中各个元素有公因子k，问k是否可以提到行列式符号外？

8、如果行列式中某一行（或某一列）中各个元素均为两项之和，此时行列式有什么样的性质？你能正确写出此公式吗？

9、对换行列式中两行（列）的位置，行列式值有什么变化？

10、行列式中的某一行（或某一列）中各个元素同乘数k后加到另一行（列）的对应元素上，行列式有何变化？

11、行列式的任何一行（列）的所有元素分别与它们所对应的代数余子式的乘积之和等于什么？

12、行列式的任何一行（列）的所有元素分别与另一行（列）对应的代数余子式的乘积之和等于什么？

13、你能叙述克拉默法则吗？应用时应该注意什么？

14、你认为这一章中的哪些实例或者练习题最有意思？哪些题目感觉较难，作为笔记的内容之一，试着总结一下.