上一节我们介绍了消元法,对于具体地解线性方程组,消元法是一个最有效和最基本的方法.但是,有时候需要直接从原方程组来看它是否有解,这样,消元法就不能用了.同时,用消元法化方程组成阶梯形,剩下来的方程的个数是否唯一决定的呢,这个问题也是没有解决的.这些问题就要求我们对线性方程组还要作进一步的研究.

显然,一个线性方程组的解的情况是被方程组中方程之间的关系所规定的,譬如说,在§1方程组

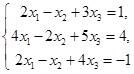
中,第一个方程的倍减去第二个方程就等于第三个方程,这就是说,第三个方程可以去掉而不影响方程组的解.在那里用初等变换得到的阶梯形方程组中只含有两个方程正是反映了这个情况.可以认为,初等变换是揭露方程之间的关系的一种方法.因此,为了直接从原来的线性方程组来讨论它解的情况,我们有必要来研究方程之间的关系.

一个元方程

可以用元有序数组

来表示,所谓方程之间的关系实际上就是代表他们的元有序数组之间的关系.因此,我们先来讨论多元有序数组.

应该指出,多元有序数组不只是可以代表线性方程,而且还与其它方面有及其广泛的联系.在解析几何中我们已经看到,有些事物的性质不能用一个数来刻画.例如,为了刻画一点在平面上的位置需要两个数,一点在空间中的位置需要三个数,也就是要知道它们的坐标.又如力学中的力、速度、加速度等,由于它们既有大小,又有方向,用一个数也不能刻画它们,在取定坐标系之后,它们可以用三个数来刻画.几何中向量的概念正是它们的抽象.但是,还有不少东西用三个数来刻画是不够的,如一个元方程组的解是由个数组成,而这个数作为方程组的解是一个整体,分开来谈是没有意义的.在几何上这样的例子也是不少的.为了刻画一个球的大小和位置,需要知道它中心坐标)(三个数)以及它的半径,也就是说,球的大小和位置需要个数来刻画.至于一个刚体的位置的确定就需要个数了.事实上,如果我们在刚体中取定一个点以及过这点的一根轴,那么刚体的位置就决定于这一点的坐标(三个数),轴的方向(两个数——它的方向余弦中的两个),以及刚体绕这根轴转动的一个角度(一个数).在国民经济的问题中,我们也会碰到这种情况.譬如一个工厂生产好几种产品,那么为了说明这个工厂的产量,就需要同时指出每种产品的产量；又如一个工厂的原料是来自好多地方,于是一个原料的采购计划就需要同时指出每个原料产地的采购量.总之,这样的例子是举不胜举的,作为它们的一个共同的抽象,我们就有

定义2 所谓数域上的一个维向量就是由数域中个数组成的有序数组

                

称为向量的分量.

几何上的向量可以认为是它的特殊情形,即且为实数域的情形.在时,维向量就没有直观的几何意义了.我们所以仍然称它为向量,一方面固然是由于它包括通常的向量作为特殊情形,另一方面也由于它与通常的向量一样可以定义运算,并且有许多运算性质是共同的,因而采取这样一个几何的名词有好处.

以后我们用小写希腊字母,,,来代表向量.

定义3  如果维向量

,

的对应分量都相等,即

,

就称两个向量是相等的,记作.

维向量之间的基本关系是用向量的加法和数量乘法表达的.

定义4  向量

称为向量

,

的和,记为

由定义立即推出：

交换律：                                

结合律：                        

定义5  分量全为零的向量

称为零向量,记为；向量称为向量的负向量,记为.

显然,对于所有的,都有            

,                     

.                   

-是向量加法的四条基本运算规律.

利用负向量,我们可以定义向量的减法.

定义6 .

定义7  设为数域中的数,向量

称为向量与数的数量乘积,记为.

由定义立即推出：

                   

                     

                         

                              

-是关于数量乘法的四条基本运算规则.由-或者由定义不难推出：

                             

                         

                             

如果,,那么

                            

定义8  以数域中的数作为分量的维向量的全体,同时考虑到定义在它们上面的加法和数量乘法,称为数域上的维向量空间.

在时,维实向量空间可以认为就是几何空间中全体向量所成的空间.

以上已把数域上全体维向量的集合组成一个有加法和数量乘法的代数结构,即数域上维向量空间.在以后的几节中将进一步讨论它的性质,并且这些性质描述和解决线性方程组中的一些问题.

向量通常是写成一行；

.

有时候也可以写成一列：

.

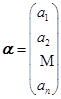为了区别,前者称为行向量,后者称为列向量.它们的区别只是写法上的不同.