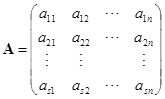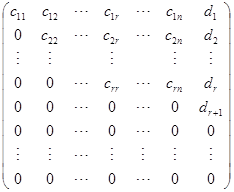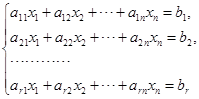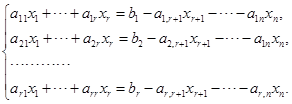当前位置:课程学习>>第四章 线性方程组>>学习内容>>视频课堂>>知识点五
知识点五:线性方程组有解的判定定理
在有了向量和矩阵的理论准备之后,我们现在可以来分析一下线性方程组解得问题,给出线性方程组有解的判定条件.
设线性方程组为
引入向量
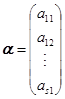 ,
,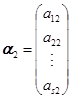 ,
,![]() ,
,
![]()
![]()
显然,线性方程组![]() 有解的充分必要条件为向量
有解的充分必要条件为向量![]() 可以表示成向量组
可以表示成向量组![]() ,
,![]() ,
,![]() ,
,![]() 的线性组合. 用秩的概念,方程组
的线性组合. 用秩的概念,方程组![]() 有解的条件可以叙述如下:
有解的条件可以叙述如下:
定理 ![]() (线性方程组有解判别定理) 线性方程组
(线性方程组有解判别定理) 线性方程组![]() 有解的充分必要条件为它的系数矩阵
有解的充分必要条件为它的系数矩阵
与增广矩阵
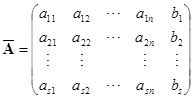
有相同的秩.
证明 先证必要性,设线性方程组![]() 有解,就是说,
有解,就是说,![]() 可以经向量组
可以经向量组![]() ,
,![]() ,
,![]() ,
,![]() 线性表出. 由此立即推出,向量组
线性表出. 由此立即推出,向量组![]() ,
,![]() ,
,![]() ,
,![]() 与向量组
与向量组![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等价,因而有相同的秩. 这两个向量组分别是矩阵
等价,因而有相同的秩. 这两个向量组分别是矩阵![]() 与
与![]() 的列向量组. 因此,矩阵
的列向量组. 因此,矩阵![]() 与
与![]() 有相同的秩.
有相同的秩.
再证充分性. 设矩阵![]() 与
与![]() 有相同的秩,就是说,它们的列向量组
有相同的秩,就是说,它们的列向量组![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 有相同的秩,令它们的秩为
有相同的秩,令它们的秩为![]() .
. ![]() ,
,![]() ,
,![]() ,
,![]() 中的极大线性无关组是由
中的极大线性无关组是由![]() 个向量组成,无妨设
个向量组成,无妨设 ![]() ,
,![]() ,
,![]() ,
,![]() 是它的一个极大线性无关组. 显然
是它的一个极大线性无关组. 显然 ![]() ,
,![]() ,
,![]() ,
,![]() 也是向量组
也是向量组![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的一个极大线性无关组,因此向量
的一个极大线性无关组,因此向量![]() 可已经
可已经![]() ,
,![]() ,
,![]() ,
,![]() 线性表出. 既然
线性表出. 既然![]() 可已经
可已经![]() ,
,![]() ,
,![]() ,
,![]() 线性表出,当然它可以经
线性表出,当然它可以经![]() ,
,![]() ,
,![]() ,
,![]() 线性表出. 因此方程组
线性表出. 因此方程组![]() 有解.
有解.
应该指出,这个判别条件与以前的消元法是一致的. 我们知道,用消元法解方程组![]() 的第一步就是用初等行变换把增广矩阵
的第一步就是用初等行变换把增广矩阵![]() 化成阶梯形. 这个阶梯形矩阵在适当调动前
化成阶梯形. 这个阶梯形矩阵在适当调动前![]() 列的顺序之后可能有两种情形:
列的顺序之后可能有两种情形:
或者 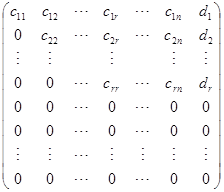 ,
,
其中![]() ,
,![]() ,
,![]() . 在前一种情形,我们说原方程组无解,而在后一种情形方程组有解. 实际上,把这个阶梯形矩阵中最后一列去掉,那就是线性方程组
. 在前一种情形,我们说原方程组无解,而在后一种情形方程组有解. 实际上,把这个阶梯形矩阵中最后一列去掉,那就是线性方程组![]() 的系数矩阵
的系数矩阵![]() 经过初等行变换所化成的阶梯形. 这就是说,当系数矩阵与增广矩阵的秩相等时,方程组有解;当增广矩阵的秩等于系数矩阵的秩加
经过初等行变换所化成的阶梯形. 这就是说,当系数矩阵与增广矩阵的秩相等时,方程组有解;当增广矩阵的秩等于系数矩阵的秩加![]() 时,方程组无解.
时,方程组无解.
以上的说明也可以认为是判别定理的另一种证明.
根据克拉默法则,也可以给出一般线性方程组的一个解法.
这个解法有时在理论上是有用的.
设线性方程组![]() 有解,矩阵
有解,矩阵![]() 与
与![]() 的秩都等于
的秩都等于![]() ,而
,而![]() 是矩阵
是矩阵![]() 的一个不为零的
的一个不为零的![]() 级子式(当然它也是
级子式(当然它也是![]() 的一个不为零的子式),为了方便起见,不妨设
的一个不为零的子式),为了方便起见,不妨设![]() 位于
位于![]() 的左上角.
的左上角.
显然,在这种情况下,![]() 的前
的前![]() 行就是一个极大线性无关组,第
行就是一个极大线性无关组,第![]() 行都可以经它们线性表出. 因此,方程组
行都可以经它们线性表出. 因此,方程组
同解.
当![]() 时,将方程组
时,将方程组![]() 改写为
改写为
![]() 作为
作为![]() 的一个方程组,它的系数行列式
的一个方程组,它的系数行列式![]() . 由克拉默法则,对于
. 由克拉默法则,对于![]() 的任意一组值,方程组
的任意一组值,方程组![]() ,也就是方程组
,也就是方程组![]() ,都有唯一的解.
,都有唯一的解. ![]() 就是方程组
就是方程组![]() 的一组自由未知量. 对
的一组自由未知量. 对![]() 用克拉默法则,可以解出
用克拉默法则,可以解出![]() :
:
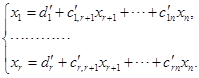
![]()
![]() 就是方程组
就是方程组![]() 的一般解.
的一般解.
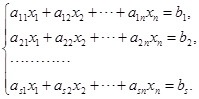
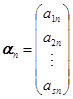 ,
,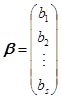 ,
,