当前位置:课程学习>>第四章 线性方程组>>学习内容>>文本学习>>知识点一
知识点一:消元法
现在来讨论一般线性方程组.所谓一般线性方程组是指形式为
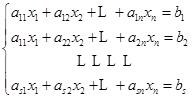
![]()
的方程组,其中![]() ,
,![]() ,
,![]() ,
,![]() 代表
代表![]() 个未知量,
个未知量,![]() 是方程的个数,
是方程的个数,![]() 称为方程组的系数,
称为方程组的系数,![]() 称为常数项.方程组中未知量的个数
称为常数项.方程组中未知量的个数![]() 与方程的个数
与方程的个数![]() 不一定相等.系数
不一定相等.系数![]() 的一个指标
的一个指标![]() 表示它在第
表示它在第![]() 个方程,第二个指标
个方程,第二个指标![]() 表示它是
表示它是![]() 的系数.
的系数.
所谓方程组![]() 的一个解就是指由
的一个解就是指由![]() 个数
个数![]() ,
,![]() ,
,![]() ,
,![]() 组成的有序数组
组成的有序数组![]() ,当
,当![]() ,
,![]() ,
,![]() ,
,![]() 分别用
分别用![]() ,
,![]() ,
,![]() ,
,![]() 带入后.
带入后.![]() 中每个等式都变成恒等式.方程组
中每个等式都变成恒等式.方程组![]() 的解的全体称为它的解集合.解方程组实际上就是找出它全部的解,或者说,求出它的解集合.如果两个方程组有相同的解集合,它们就称为同解的.
的解的全体称为它的解集合.解方程组实际上就是找出它全部的解,或者说,求出它的解集合.如果两个方程组有相同的解集合,它们就称为同解的.
显然,如果知道了一个线性方程组的全部系数和常数项,那么这个线性方程组就基本上确定了.确切地说,线性方程组可以用下面的矩阵
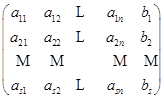
![]()
来表示.实际上,有了![]() 之后,除去代表未知量的文字外,线性方程组
之后,除去代表未知量的文字外,线性方程组![]() 就确定了,而采用什么文字来表示未知量当然不是实质性的.在中学所学代数里我们学过用加减消元法解二元、三元线性方程组.实际上,这个方法比用行列式解方程组更具有普遍性.下面就来介绍如何用一般消元法解一般线性方程组.
就确定了,而采用什么文字来表示未知量当然不是实质性的.在中学所学代数里我们学过用加减消元法解二元、三元线性方程组.实际上,这个方法比用行列式解方程组更具有普遍性.下面就来介绍如何用一般消元法解一般线性方程组.
先看一个例子
例如,解方程组
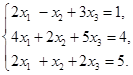
第二个方程减去第一个方程的![]() 倍,第三个方程减去第一个方程,就变成
倍,第三个方程减去第一个方程,就变成
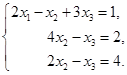
第二个方程减去第三个方程的![]() 倍,把第二第三两个方程的次序互换,即得
倍,把第二第三两个方程的次序互换,即得
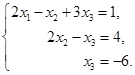
这样,我们就容易求出方程组的解为![]() .
.
分析一下消元法,不难看出,它实际上是反复地对方程组进行变换,而所作的变换也只是由以下三种基本的变化所构成:
1.用一非零的数乘某一方程;
2.把一个方程的倍数加到另一个方程;
3.互换两个方程的位置.
于是,我们给出:
定义1 变换![]() 称为线性方程组的初等变换.
称为线性方程组的初等变换.
消元的过程就是反复施行初等变换的过程.下面证明,初等变换总是把方程组变成同解的方程组.我们只对第二种初等变换来证明.
对方程组
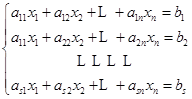
![]()
进行第二种初等变换.为简便起见,不妨设把第二个方程的![]() 倍加到第一个方程得到新方程组
倍加到第一个方程得到新方程组
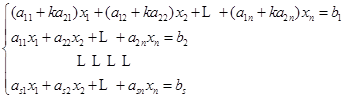
![]()
现在设![]() 是
是![]() 的任一解.因
的任一解.因![]() 与
与![]() 的后
的后![]() 个方程.又
个方程.又![]() 满足
满足![]() 的前两个方程
的前两个方程
![]() ,
,
![]() .
.
把第二式的两边乘以![]() ,再与第一式相加,即为
,再与第一式相加,即为
![]() .
.
故![]() 又满足
又满足![]() 的第一个方程,因而是
的第一个方程,因而是![]() 的解.类似地可证
的解.类似地可证![]() 的任一解也是
的任一解也是![]() 的解.这就证明了
的解.这就证明了![]() 与
与![]() 是同解的.
是同解的.
对另外两种初等变换,证明由读者去做.
下面我们来说明,如何利用初等变换来解一般的线性方程组.
对于方程组![]() ,首先检查
,首先检查![]() 的系数.如果
的系数.如果![]() 的系数
的系数![]() ,
,![]() ,
,![]() ,
,![]() 全为零,那么方程组
全为零,那么方程组![]() 对
对![]() 没有任何限制,
没有任何限制,![]() 就可以取任意值,而方程组
就可以取任意值,而方程组![]() 可以看作
可以看作![]() ,
,![]() ,
,![]() 的方程组来解.如果
的方程组来解.如果![]() 的系数不全为零,那么利用初等变换
的系数不全为零,那么利用初等变换![]() ,可以设
,可以设![]() .利用初等变换
.利用初等变换![]() ,分别地把第一个方程的
,分别地把第一个方程的![]() 倍加到第
倍加到第![]() 个方程
个方程![]() .于是方程组
.于是方程组![]() 就变成
就变成
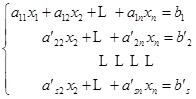
![]()
其中
![]() ,
,![]() ,
,![]() .
.
这样,解方程组![]() 的问题就归结为解方程组
的问题就归结为解方程组
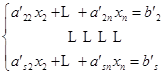
![]()
的问题.显然,![]() 的一个解,带入
的一个解,带入![]() 的第一个方程就定出
的第一个方程就定出![]() 的值,这就得出
的值,这就得出![]() 的一个解;而
的一个解;而![]() 的解显然都是
的解显然都是![]() 的解.这就是说,方程组
的解.这就是说,方程组![]() 有解的充分必要条件为方程组
有解的充分必要条件为方程组![]() 有解,而
有解,而![]() 与
与![]() 是同解的,因之,方程组
是同解的,因之,方程组![]() 有解的充分必要条件为方程组
有解的充分必要条件为方程组![]() 有解.
有解.
对![]() 再按上面的考虑进行变换,并且这样一步步作下去,最后就得到一个阶梯形方程组.为了讨论起来方便,不妨设所得到的方程组为
再按上面的考虑进行变换,并且这样一步步作下去,最后就得到一个阶梯形方程组.为了讨论起来方便,不妨设所得到的方程组为
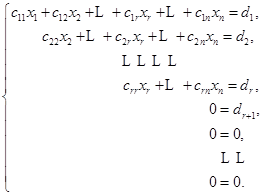
![]()
其中![]() ,
,![]() .方程组
.方程组![]() 中的“
中的“![]() ”这样一些恒等式可能不出现,也可能出现,这时去掉它们也不影响
”这样一些恒等式可能不出现,也可能出现,这时去掉它们也不影响![]() 的解.而且
的解.而且![]() 与
与![]() 是同解的.
是同解的.
现在考察![]() 的解的情况.
的解的情况.
如![]() 中有方程
中有方程![]() ,而
,而![]() .这时不管
.这时不管![]() ,
,![]() ,
,![]() 取什么值都不能使它成为等式.故
取什么值都不能使它成为等式.故![]() 无解,因而
无解,因而![]() 无解.
无解.
当![]() 是零或
是零或![]() 中根本没有“
中根本没有“![]() ”的方程时,分两种情况:
”的方程时,分两种情况:
1) ![]() .这时阶梯形方程组为
.这时阶梯形方程组为
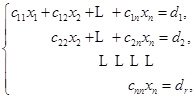
![]()
其中![]() ,
,![]() .由最后一个方程开始,
.由最后一个方程开始,![]() ,
,![]() ,
,![]() ,
,![]() 的值就可以逐个地唯一地决定了.在这个情形,方程组
的值就可以逐个地唯一地决定了.在这个情形,方程组![]() ,也就是方程组
,也就是方程组![]() 有唯一的解.
有唯一的解.
例1 上面讨论过的方程组
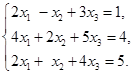
经过一系列初等变换后,它变成了阶梯形方程组
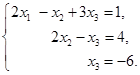
把![]() 代入第二个方程,得
代入第二个方程,得
![]() .
.
再把![]() ,
,![]() 代入第一个方程,即得
代入第一个方程,即得
![]() .
.
这就是说,上述方程组有唯一的解![]() .
.
1) ![]() .这时阶梯形方程组为
.这时阶梯形方程组为
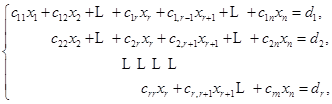
其中![]() ,
,![]() .把它改写成
.把它改写成
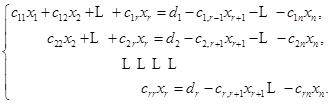
![]()
由此可见,任给![]() ,
,![]() ,
,![]() 一组值,就唯一地定出
一组值,就唯一地定出![]() ,
,![]() ,
,![]() ,
,![]() 的值,也就是定出方程组
的值,也就是定出方程组![]() 的一个解,一般地,由
的一个解,一般地,由![]() 我们可以把
我们可以把![]() ,
,![]() ,
,![]() ,
,![]() 通过
通过![]() ,
,![]() ,
,![]() 表示出来,这样一组表达式称为方程组
表示出来,这样一组表达式称为方程组![]() 的一般解,而
的一般解,而![]() ,
,![]() ,
,![]() 称为一组自由未知量.
称为一组自由未知量.
例2 解方程组
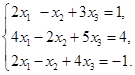
用初等变换消去,得
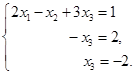
改写一下,
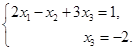
![]()
最后得
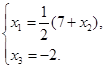
这就是方程组![]() 的一般解,其中
的一般解,其中![]() 是自由未知量.
是自由未知量.
从这个例子看出,一般线性方程组化成阶梯形,不一定就是![]() 的样子,但是只要把方程组中的某些项调动一下,总可以化成
的样子,但是只要把方程组中的某些项调动一下,总可以化成![]() 的样子.
的样子.
应该看到,![]() 的情形是不可能出现的.
的情形是不可能出现的.
以上就是用消元法解线性方程组的整个过程.总起来说就是,首先用初等变换化线性方程组为阶梯形方程组,把最后的一些恒等式“![]() ”(如果出现的话)去掉.如果剩下的方程当中最后的一个等式是零等于一非零的数,那么方程组无解,否则有解.在有解的情况下,如果阶梯形方程组中方程的个数
”(如果出现的话)去掉.如果剩下的方程当中最后的一个等式是零等于一非零的数,那么方程组无解,否则有解.在有解的情况下,如果阶梯形方程组中方程的个数![]() 等于未知量的个数,那么方程组有唯一的解;如果阶梯形方程组中方程的个数
等于未知量的个数,那么方程组有唯一的解;如果阶梯形方程组中方程的个数![]() 小于未知量的个数,那么方程组就有无穷多个解.
小于未知量的个数,那么方程组就有无穷多个解.
把以上结果应用到齐次线性方程组,就有
定理1 在齐次线性方程组
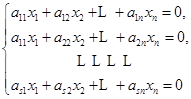
中,如果![]() ,那么它必有非零解.
,那么它必有非零解.
证明 显然,方程组在化成阶梯形方程组之后,方程的个数不会超过原方程组中方程的个数,即
![]() .
.
由![]() 得知,它的解不是唯一的,因而必有非零解.
得知,它的解不是唯一的,因而必有非零解.
矩阵
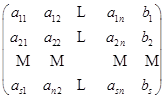
![]()
称为线性方程组![]() 的增广矩阵.显然,用初等变换化方程组
的增广矩阵.显然,用初等变换化方程组![]() 成阶梯形就相当于用初等变换化方程组
成阶梯形就相当于用初等变换化方程组![]() 成阶梯形矩阵.因此,解线性方程组的第一步工作可以通过矩阵来进行,而从化成的阶梯形矩阵就可以判别方程组有解还是无解,在有解的情形,回到阶梯形方程组去解.
成阶梯形矩阵.因此,解线性方程组的第一步工作可以通过矩阵来进行,而从化成的阶梯形矩阵就可以判别方程组有解还是无解,在有解的情形,回到阶梯形方程组去解.
例3 解
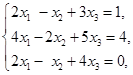
对它的增广矩阵作初等行变换,
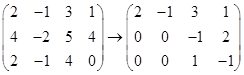
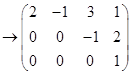
从最后一行![]() 可以看出原方程组无解.
可以看出原方程组无解.
