当前位置:课程学习>>第四章 线性方程组>>学习内容>>文本学习>>知识点三
知识点三:线性相关性
以下我们总是在一固定的数域![]() 上的
上的![]() 维向量空间中进行讨论,不再每次说明了.
维向量空间中进行讨论,不再每次说明了.
在这一节我们来进一步研究向量之间的关系.两个向量之间最简单的关系是成比例.所谓向量![]() 与
与![]() 成比例就是说有一数
成比例就是说有一数![]() 使
使
![]() .
.
在多个向量之间,成比例的关系表现为线性组合.
定义9 向量![]() 称为向量组
称为向量组![]() ,
,![]() ,
,![]() ,
,![]() 的一个线性组合,如果有数域
的一个线性组合,如果有数域![]() 中的数
中的数![]() ,
,![]() ,
,![]() ,
,![]() ,使
,使
![]() .
.
例如,§1的方程组![]() 的三个方程可以用向量
的三个方程可以用向量
![]() ,
, ![]() ,
,
![]()
来代表.我们知道,第![]() 个方程等于第
个方程等于第![]() 个方程的
个方程的![]() 倍减去第
倍减去第![]() 个方程,这等价于
个方程,这等价于![]() .这个等式表示
.这个等式表示![]() 是
是![]() ,
,![]() 的一个线性组合.
的一个线性组合.
又如,任一个![]() 维向量
维向量![]() 都是向量组
都是向量组
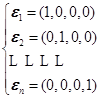
![]()
的一个线性组合.因为
![]() .
.
向量![]() ,
,![]() ,
,![]() ,
,![]() 称为
称为![]() 维单位向量.
维单位向量.
由定义可以立即看出,零向量是任一向量组的线性组合(只要系数全为![]() 就行了).
就行了).
当向量![]() 是向量组
是向量组![]() ,
,![]() ,
,![]() ,
,![]() 的一个线性组合时,我们也说
的一个线性组合时,我们也说![]() 可以经向量组
可以经向量组![]() ,
,![]() ,
,![]() ,
,![]() 线性表出.
线性表出.
定义10 如果向量组![]() ,
,![]() ,
,![]() ,
,![]() 中每一个向量
中每一个向量![]() 都可以经向量组
都可以经向量组![]() ,
,![]() ,
,![]() ,
,![]() 线性表出,那么向量组
线性表出,那么向量组![]() ,
,![]() ,
,![]() ,
,![]() 就称为可以经向量组
就称为可以经向量组![]() ,
,![]() ,
,![]() ,
,![]() 线性表出.如果两个向量组互相可以线性表出,它们就称为等价.
线性表出.如果两个向量组互相可以线性表出,它们就称为等价.
例如,设
![]() ,
,![]()
![]() ,
,![]()
则向量组![]() ,
,![]() 与向量组
与向量组![]() ,
,![]() 是等价的.
是等价的.
由定义不难证明,每一个向量组都可以经它自身线性表出.同时,如果向量组![]() ,
,![]() ,
,![]() ,
,![]() 可以经由向量组
可以经由向量组![]() ,
,![]() ,
,![]() ,
,![]() 线性表出.向量组
线性表出.向量组![]() ,
,![]() ,
,![]() ,
,![]() 可以经由
可以经由![]() ,
,![]() ,
,![]() ,
,![]() 线性表出,那么向量组
线性表出,那么向量组![]() ,
,![]() ,
,![]() ,
,![]() 可以经由
可以经由![]() ,
,![]() ,
,![]() ,
,![]() 线性表出.
线性表出.
事实上,如果
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
, ![]() .
.
这就是说,向量组![]() ,
,![]() ,
,![]() ,
,![]() 中每一个向量都可以经过向量组
中每一个向量都可以经过向量组![]() ,
,![]() ,
,![]() ,
,![]() 线性表出,因而向量组
线性表出,因而向量组![]() ,
,![]() ,
,![]() ,
,![]() 可以经向量组
可以经向量组![]() ,
,![]() ,
,![]() ,
,![]() 线性表出.
线性表出.
由上述的结论,得知向量组之间的等价有以下性质:
1) 反身性:每一个向量组都与它自身等价.
2) 对称性:如果向量组![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]() 等价,那么向量组
等价,那么向量组![]() ,
,![]() ,
,![]() ,
,![]() 也与
也与![]() ,
,![]() ,
,![]() ,
,![]() 等价.
等价.
3) 传递性:如果向量组![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]() 等价,
等价,![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]() 等价,那么向量组
等价,那么向量组![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]() 等价.
等价.
定义11 如果向量组![]() ,
,![]() ,
,![]() ,
,![]()
![]() 中有一个向量可以由其余的向量线性表出,那么向量组
中有一个向量可以由其余的向量线性表出,那么向量组![]() ,
,![]() ,
,![]() ,
,![]() 就称为线性相关的.
就称为线性相关的.
例如,向量组![]() ,
,![]() ,,
,,![]() 是线性相关的,因为
是线性相关的,因为
![]() .
.
从定义可以看出,任意一个包含零向量的向量组一定是线性相关的.还可看出,向量组![]() ,
,![]() 线性相关就表示
线性相关就表示![]() 或者
或者![]() (这两个式子不一定能同时成立).在
(这两个式子不一定能同时成立).在![]() 为实数域,并且是三维的情形,这就表示向量
为实数域,并且是三维的情形,这就表示向量![]() 与
与![]() 共线,三个向量
共线,三个向量![]() ,
,![]() ,
,![]() 线性相关的几何意义就是他们共面,因为由定义,其中一个向量是另外几个的线性组合,譬如
线性相关的几何意义就是他们共面,因为由定义,其中一个向量是另外几个的线性组合,譬如
![]() ,
,
这就是说,![]() 在
在![]() 与
与![]() 所在的平面上.
所在的平面上.
向量组的线性相关的定义还可以用另一个说法:
定义11' 向量组![]() ,
,![]() ,
,![]() ,
,![]()
![]() 称为线性相关,如果有数域
称为线性相关,如果有数域![]() ,中不全为零的数
,中不全为零的数![]() ,
,![]() ,
,![]() ,
,![]() ,使
,使
![]() .
.
现在我们来证明这两个定义在![]() 的时候是一致的.
的时候是一致的.
如果向量组![]() ,
,![]() ,
,![]() ,
,![]() ,按定义11'是线性相关的,那么其中有一个向量是其余向量的线性组合,譬如说
,按定义11'是线性相关的,那么其中有一个向量是其余向量的线性组合,譬如说
![]() .
.
把它改写一下,就有
![]() .
.
因为数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 不全为
不全为![]() (至少
(至少![]() ),所以按定义11,这个向量组线性相关.
),所以按定义11,这个向量组线性相关.
反过来,如果向量组![]() ,
,![]() ,
,![]() ,
,![]() ,按定义11线性相关,即有不全为零的数
,按定义11线性相关,即有不全为零的数![]() ,
,![]() ,
,![]() ,
,![]() ,使
,使
![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,![]() 不全为零,不妨设
不全为零,不妨设![]() ,于是上式可以改写为
,于是上式可以改写为
![]() .
.
这就是说,向量![]() 可以被其余的向量线性表出,所以此向量组按定义11'也线性相关.
可以被其余的向量线性表出,所以此向量组按定义11'也线性相关.
定义12 一向量组![]() ,
,![]() ,
,![]() ,
,![]()
![]() 不线性相关,即没有不全为零的数
不线性相关,即没有不全为零的数![]() ,
,![]() ,
,![]() ,
,![]() 使
使
![]() .
.
就称为线性无关;或者说,一向量组![]() ,
,![]() ,
,![]() ,
,![]() 称为线性无关,如果由
称为线性无关,如果由
![]()
可以推出
![]() .
.
由定义立即得出,如果一向量组的一部分线性相关,那么这个向量组就线性相关.设向量组为![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ,其中一部分,譬如说
,其中一部分,譬如说![]() ,
,![]() ,
,![]() ,
,![]() 线性相关,即有不全为
线性相关,即有不全为![]() 的数
的数![]() ,
,![]() ,
,![]() ,
,![]() 使
使
![]() .
.
由上式显然有
![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,![]() 不全为
不全为![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 也不全为零,因而
也不全为零,因而![]() ,
,![]() ,
,![]() ,
,![]() 线性相关,
线性相关,
换个说法,如果一向量组线性无关,那么它的任何一个非空的部分组也线性无关.特别地,由于两个成比例的向量是线性相关的,所以,线性无关的向量组中一定不能包含两个成比例的向量.
定义11包含了由一个向量构成的向量组的情形.按定义向量组![]() 线性相关就表示有
线性相关就表示有![]() (因为只有一个数,所以不全为零就是它不等于零)使
(因为只有一个数,所以不全为零就是它不等于零)使
![]() .
.
由数乘的性质推知![]() .因此,向量组
.因此,向量组![]() 线性相关就表示
线性相关就表示![]() .
.
不难看出,由![]() 维向量
维向量![]() ,
,![]() ,
,![]() ,
,![]() 组成的向量组是线性无关的.事实上,由
组成的向量组是线性无关的.事实上,由
![]() ,
,
也就是由
![]()
![]()
![]()
可以推出
![]() .
.
这就是说,![]() ,
,![]() ,
,![]() ,
,![]() 线性无关.
线性无关.
具体判断一个向量组是线性相关还是线性无关的问题可以归结为解方程组 的问题.我们考察已经碰到过的例子,判断向量组
![]() ,
,![]() ,
,![]() 是否线性相关.
是否线性相关.
可取![]() ,
,![]() ,
,![]() 为未知数,建立下列方程式
为未知数,建立下列方程式
![]()
看它是否有![]() ,
,![]() ,
,![]() 的不全为零的解.这是向量等式,按各个分量分别写出方程,就成为下列方程组:
的不全为零的解.这是向量等式,按各个分量分别写出方程,就成为下列方程组:
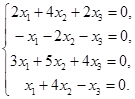
前面的含向量的方程有无非零解等价于这个方程有无非零解.可以用消元法解这个方程组.它有无限多解,当然有非零解.故![]() ,
,![]() ,
,![]() 线性相关.特别的一组解,可取为
线性相关.特别的一组解,可取为![]() .即
.即![]() ,或
,或![]() .这是前面已指出的结果.
.这是前面已指出的结果.
一般地,要判别一个向量组
![]() ,
,![]() .
. ![]()
是否线性相关,根据定义11,就是看方程
![]()
![]()
有无非零解.![]() 式按分量写出来就是
式按分量写出来就是
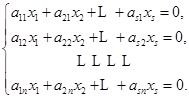
![]()
因之,向量组![]() ,
,![]() ,
,![]() ,
,![]() 线性无关的充分必要条件是齐次线性方程组
线性无关的充分必要条件是齐次线性方程组![]() 只有零解.
只有零解.
从这里很容易看出,如果向量组![]() 线性无关,那么每一个向量上添一个分量所得到的
线性无关,那么每一个向量上添一个分量所得到的![]() 维的向量组
维的向量组
![]() ,
,![]()
![]()
也线性无关.
事实上,与向量组![]() 相对应的齐次线性方程组为
相对应的齐次线性方程组为
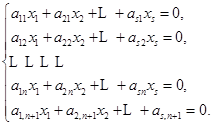
显然,方程组![]() 的解全是方程组
的解全是方程组![]() 的解,如果
的解,如果![]() 只有零解,那么
只有零解,那么![]() 也只有零解.
也只有零解.
这个结果当然可以推广到添几个分量的情形.
利用§1的定理1,即得向量组的一个基本性质.
定理2 设![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]() 是两个向量组,如果
是两个向量组,如果
1) 向量组![]() ,
,![]() ,
,![]() ,
,![]() 可以经
可以经![]() ,
,![]() ,
,![]() ,
,![]() 线性表出线性表出,
线性表出线性表出,
2) ![]() ,
,
那么向量组![]() ,
,![]() ,
,![]() ,
,![]() 必线性相关.
必线性相关.
证明 由1)有
![]() ,
,![]() .
.
为此,我们作线性组合
![]()
![]() .
.
如果我们能找到不全为零的数![]() ,
,![]() ,
,![]() ,
,![]() 使
使![]() ,
,![]() ,
,![]() ,
,![]() 的系数全为零,那就证明了
的系数全为零,那就证明了![]() ,
,![]() ,
,![]() ,
,![]() 的线性相关性.这一点是能够做到的,因为由2),即
的线性相关性.这一点是能够做到的,因为由2),即![]() ,齐次方程组
,齐次方程组
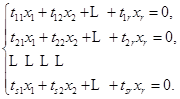
把定理2换个说法,即得:
推论1 如果向量组![]() ,
,![]() ,
,![]() ,
,![]() 可以经向量组
可以经向量组![]() ,
,![]() ,
,![]() ,
,![]() 线性表出,且
线性表出,且![]() ,
,![]() ,
,![]() ,
,![]() 线性无关,那么
线性无关,那么![]() .
.
直接应用定理2,即得:
推论2 任意![]() 个
个![]() 维向量必线性相关.
维向量必线性相关.
事实上,每个![]() 维向量都可以被
维向量都可以被![]() 维单位向量
维单位向量![]() ,
,![]() ,
,![]() ,
,![]() 线性表出,且
线性表出,且![]() ,因而必线性相关.
,因而必线性相关.
由推论1,得:
推论3 两个线性无关的等价向量组,必含有相同个数的向量.
定理2的几何意义是清楚的:子啊三维向量的情形,如果![]() ,那么可以由向量
,那么可以由向量![]() ,
,![]() 线性表出的向量当然都在
线性表出的向量当然都在![]() ,
,![]() 所在的平面上,因而这些向量是共面的,也就是,当
所在的平面上,因而这些向量是共面的,也就是,当![]() 时,这些向量线性相关.两个向量组
时,这些向量线性相关.两个向量组![]() ,
,![]() 与
与![]() ,
,![]() 等价,就意味着它们在同一平面上.
等价,就意味着它们在同一平面上.
定义13 一向量组的一个部分组称为一个极大线性无关组,如果这个部分组本身是线性无关的,并且从这个向量组中任意添一个向量(如果还有的话),所得的部分向量组都线性相关.
例如,在向量组![]() ,
,![]() ,,
,,![]() 中,由
中,由![]() ,
,![]() 组成的部分组就是一个极大线性无关组.首先,
组成的部分组就是一个极大线性无关组.首先,![]() ,
,![]() 线性无关,因为由
线性无关,因为由
![]()
![]()
就有![]() .同时我们知道,
.同时我们知道,![]() ,
,![]() ,
,![]() 线性相关.不难看出,
线性相关.不难看出,![]() ,
,![]() 也是一个极大线性无关组(请读者验证一下).
也是一个极大线性无关组(请读者验证一下).
应该看到,一个线性无关向量组的极大线性无关组就是这个向量组自身.
极大线性无关组的一个基本性质是,任意一个极大线性无关组都与向量组本身等价.
事实上,设向量组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,而
,而![]() ,
,![]() ,
,![]()
![]() 是它的一个极大线性无关组.所谓等价就是它们可以互相线性表出,即,
是它的一个极大线性无关组.所谓等价就是它们可以互相线性表出,即,
![]() ,
, ![]()
因此,问题在于![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是否可以被
是否可以被![]() ,
,![]() ,
,![]()
![]() 线性表出.向量
线性表出.向量![]() ,
,![]() ,
,![]()
![]() 中每一个都可以被
中每一个都可以被![]() ,
,![]() ,
,![]() ,
,![]() 线性表出是显然的.现在来看
线性表出是显然的.现在来看![]() ,
,![]() ,
,![]() 中的向量,设
中的向量,设![]() 是这样一个向量.由极大线性无关组
是这样一个向量.由极大线性无关组![]() ,
,![]() ,
,![]() 的极大性,向量组
的极大性,向量组![]() ,
,![]() ,
,![]() ,
,![]() 线性相关,也就是说,有不全为零的数
线性相关,也就是说,有不全为零的数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 使
使
![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,![]() 是线性无关的,可证必有
是线性无关的,可证必有![]() .否则,设
.否则,设![]() ,那么
,那么![]() ,
,![]() ,
,![]() ,
,![]() 就不全为零,于是
就不全为零,于是![]() ,
,![]() ,
,![]() ,
,![]() 就线性相关,这与假设矛盾.由
就线性相关,这与假设矛盾.由![]() ,上式可以改写为
,上式可以改写为
![]()
![]() .
.
这就是说,![]() 可以被
可以被![]() ,
,![]() ,
,![]() ,
,![]() 线性表出.于是证明了向量组与它的极大线性无关组的等价性.
线性表出.于是证明了向量组与它的极大线性无关组的等价性.
由上面的例子可以看到,向量组的极大线性无关组不是唯一的.但是每一个极大线性无关组都与向量组本身等价,因而,一向量组的任意两个极大线性无关组都是等价的,虽然极大线性无关组可以有很多,但是由定理2的推论3,立即得出
定理3 一向量组的极大线性无关组都含有相同个数的向量.
定理3表明,极大线性无关组所含向量的个数与极大线性无关组 的选择无关,它直接反映了向量组本身的性质.因此,我们有
定义14 向量组的极大线性无关组所含向量个数称为这个向量组的秩.
例如,向量组![]() ,
,![]() ,
,![]() 的秩就是
的秩就是![]() .
.
因为线性无关的向量组就是他们自身的极大线性无关组,所以一向量组线性无关的充分必要条件为它的秩与它所含向量的个数相同.
我们知道,每一向量都与它的极大线性无关组等价.由等价的传递性可知,任意两个等价向量组的极大线性无关组也等价.所以,等价的向量组必有相同的秩.
还要指出:含有非零向量的向量组一定有极大线性无关组,且任意个无关的部分向量组都能扩充成一个极大线性无关组(参见习题9).全部由零向量组成的向量组没有极大线性无关组.我们规定这样的向量组的秩为零.
现在把上面的概念与方程组的解的关系进行联系,给定一个方程组
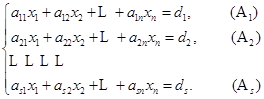
各个方程所对应的向量分别是![]() ,
,![]() ,
,![]() ,
,![]()
![]() .设有另一方程
.设有另一方程
![]()
![]()
它对应的向量为
![]() .则
.则![]() 是
是![]() ,
,![]() ,
,![]() ,
,![]() 的线性组合,
的线性组合,![]() 当且仅当
当且仅当![]() ,即方程
,即方程![]() 是方程
是方程![]() ,
,![]() ,
,![]() ,
,![]() 的线性组合.容易验证,方程组
的线性组合.容易验证,方程组![]() ,
, ![]() ,
,![]() 的解一定满足
的解一定满足![]() .进一步设方程组
.进一步设方程组
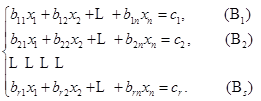
它的方程所对应的向量为![]() ,
,![]() ,
,![]() ,
,![]() .若
.若![]() ,
,![]() ,
,![]() ,
,![]() 可经
可经![]() ,
,![]() ,
,![]() ,
,![]() 线性表出,则方程组
线性表出,则方程组![]() ,
,![]() ,
,![]() ,
,![]() 的解是方程组
的解是方程组![]() ,
,![]() ,
,![]() ,
,![]() 的解.再进一步,当
的解.再进一步,当![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]() 等价时,两个方程组同解.
等价时,两个方程组同解.
