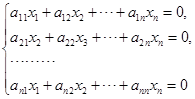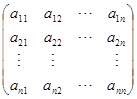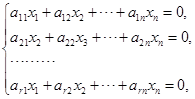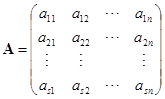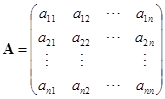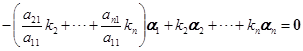当前位置:课程学习>>第四章 线性方程组>>学习内容>>文本学习>>知识点四
知识点四:矩阵的秩
在上一节我们定义了向量组的秩,如果我们把矩阵的每一行看成一个向量,那么矩阵就可以认为是有这些行向量组成的. 同样,如果把每一列看成一个向量,那么矩阵也可以认为是由列量组成的.
定义 15 所谓矩阵的行秩就是指矩阵的行向量组的秩;矩阵的列秩就是矩阵的列向量组的秩.
例如,矩阵
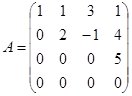
的列向量组是
![]() ,
, ![]()
![]() ,
, ![]() .
.
组. 事实上,由
![]() ,
,
即
![]()
![]() ,
,
可得![]() ,这就证明了
,这就证明了![]() ,
,![]() ,
,![]() 线性无关. 因为
线性无关. 因为![]() 是零向量,所以把
是零向量,所以把![]() 添进去就线性相关了,因此,向量组
添进去就线性相关了,因此,向量组![]() ,
,![]() ,
,![]() ,
,![]() 的秩为3,也就是说,矩阵
的秩为3,也就是说,矩阵![]() 的秩为3.
的秩为3. ![]() 的 列向量组是
的 列向量组是
![]() ,
,![]() .
.
用同样的方法可证,![]() ,
,![]() ,
,![]() 线性无关而
线性无关而![]() ,所以把
,所以把![]() 添进去就线性相关了. 因之,
添进去就线性相关了. 因之,![]() ,
,![]() ,
,![]() 是向量组
是向量组![]() ,
,![]() ,
,![]() ,
,![]() 的一个极大线性无关组,于是向量组
的一个极大线性无关组,于是向量组![]() ,
,![]() ,
,![]() ,
,![]() 的秩为3. 换句话说,矩阵
的秩为3. 换句话说,矩阵![]() 的秩也是3.
的秩也是3.
矩阵![]() 的行秩等于列秩,这一点不是偶然的,下面来一般地证明行秩与列秩是相等的.
的行秩等于列秩,这一点不是偶然的,下面来一般地证明行秩与列秩是相等的.
作为一个准备,我们先利用行秩的概念把定理1(§1)改进如下.
引理 如果齐次线性方程组
的系数矩阵
的行秩![]() ,那么它有非零解.
,那么它有非零解.
为![]() ,所以极大线性无关组是由
,所以极大线性无关组是由![]() 个向量组成. 无妨设
个向量组成. 无妨设![]() ,
,![]() ,
,![]()
是一个极大线性无关组. 我们知道,向量组![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() ,
,![]() ,
,![]() 是等价的,也就是说,方程组
是等价的,也就是说,方程组![]() 与方程组
与方程组
可以互相线性表出,因而方程组![]() 与
与![]() 同解. 对于方程组
同解. 对于方程组![]() 应用§1定理1,即得所要的结论.
应用§1定理1,即得所要的结论.
由此就可以证明:
定理4 矩阵的行秩与列秩相等.
证明 设所讨论的矩阵为
以![]() ,
,![]() ,
,![]() ,
,![]() 代表矩阵
代表矩阵![]() 的行向量组,无妨设
的行向量组,无妨设![]() ,
,![]() ,
,![]() 是它的一个极大线性无关组. 因为
是它的一个极大线性无关组. 因为![]() ,
,![]() ,
,![]() 是线性无关的,所以方程
是线性无关的,所以方程
![]()
只有零解,这也就是说,齐次线性方程组
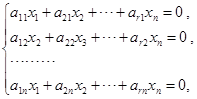
只有零解. 由引理,这个方程的系数矩阵
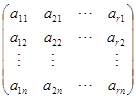
的行秩![]()
![]() . 因之在它的行向量中可以找到
. 因之在它的行向量中可以找到![]() 个是线性无关的,譬如说,向量组
个是线性无关的,譬如说,向量组
线性无关. 根据上一节的说明,在这些向量上添加几个分量后所得的向量组
![]() ,
,![]() ,
,
![]() ,
,![]()
也线性无关. 它们正好是矩阵![]() 的
的![]() 个列向量,由它们的线性无关性可知矩阵
个列向量,由它们的线性无关性可知矩阵![]() 的列秩
的列秩![]() 至少是
至少是![]() ,也就是说
,也就是说![]() .
.
用同样的方法可证![]() . 这样,我们就证明了行秩与列秩的相等.
. 这样,我们就证明了行秩与列秩的相等.
因为行秩等于列秩,所以下面就称为矩阵的秩.
现在我们再来把矩阵的秩与行列式的概念联系起来. 先看![]() 矩阵的情形.
矩阵的情形.
定理 ![]()
![]() 矩阵
矩阵
的行列式为零的充分必要条件是![]() 的秩小于
的秩小于![]() .
.
证明 先证充分性. 因为![]() 的秩小于
的秩小于![]() ,所以
,所以![]() 得
得![]() 个行向量组线性无关. 当
个行向量组线性无关. 当![]() 时,
时,![]() 只有一个数,即只有一个一维向量,
只有一个数,即只有一个一维向量,
它又是线性相关的向量组,就是零向量,从而![]() . 当
. 当![]() 时,矩阵
时,矩阵![]() 中有一行是其余各行的线性组合. 由行列式的性质可知
中有一行是其余各行的线性组合. 由行列式的性质可知![]() .
.
假设结论对![]() 级矩阵已证,现在来看
级矩阵已证,现在来看![]() 级矩阵的情况.我们以
级矩阵的情况.我们以![]() ,
,![]() ,
,![]() ,
,![]() 代表
代表![]() 的行向量. 检查
的行向量. 检查![]() 的第一列的元素
的第一列的元素![]() ,如果他们全为零,那么
,如果他们全为零,那么![]() 的列向量组中含有零向量,当然秩小于
的列向量组中含有零向量,当然秩小于![]() . 如果这
. 如果这![]() 个元素中有一个不为零,譬如说
个元素中有一个不为零,譬如说![]() ,那么从第二行直到第
,那么从第二行直到第![]() 行减去第一行的适当的倍数,把
行减去第一行的适当的倍数,把
![]() 消成零,即得
消成零,即得
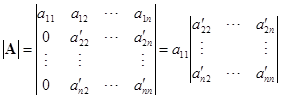 ,
,
其中
![]() ,
,![]() .
.
由![]() 可知
可知![]() 级矩阵
级矩阵
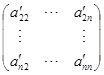
的行列式为零. 根据归纳法假定,这个矩阵的行向量线性相关. 因而向量组
![]()
线性相关,这就是说,有不全为零的数![]() 使
使
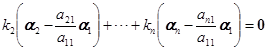 .
.
改写一下,有
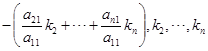 这组数当然也不全为零,从而向量组
这组数当然也不全为零,从而向量组![]() ,
,![]() ,
,![]() ,
,![]() 线性相关,它的秩小于
线性相关,它的秩小于![]() .
.
根据归纳法原理必要性得证.
根据这个定理,可以得到有关齐次线性方程组的重要结论.
推论 齐次线性方程组
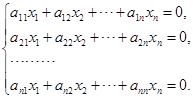
有非零解的充分必要条件是它的系数矩阵
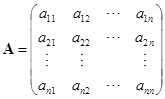
的行列式等于零.
证明 条件的充分性可以由定理![]() 及引理直接得出。
及引理直接得出。
条件的必要性是克拉默法则的直接推论.
为了建立一般矩阵的秩跟行列式的关系,我们引入
定义 ![]() 在一个
在一个![]() 矩阵
矩阵![]() 中任意选定
中任意选定![]() 行和
行和![]() 列,位于这些选定的行和列的交点上的
列,位于这些选定的行和列的交点上的![]() 个元素按原来的次序所组成的
个元素按原来的次序所组成的![]() 级行列式,称为
级行列式,称为![]() 的一个
的一个![]() 级子式.
级子式.
例 在矩阵
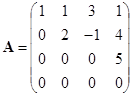
中,选第![]() 行和第
行和第![]() 列,它们交点上的元素所成的二级行列式
列,它们交点上的元素所成的二级行列式
![]()
就是一个二级子式. 又如选第![]() 行和第
行和第![]() 列,相应的
列,相应的![]() 级子式就是
级子式就是
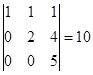 .
.
由于行和列的选法很多,所以![]() 级子式也是很多的.矩阵的秩与行列式的关系表现为:
级子式也是很多的.矩阵的秩与行列式的关系表现为:
定理 ![]() 一矩阵的秩是
一矩阵的秩是![]() 的充分必要条件为矩阵中有一个
的充分必要条件为矩阵中有一个![]() 级子式不为零,同时所有
级子式不为零,同时所有![]() 级子式全为零.
级子式全为零.
证明 先证必要性. 设矩阵![]() 的秩为
的秩为![]() . 这时由定理
. 这时由定理![]() 知矩阵
知矩阵![]() 中任意
中任意![]() 个行向量都线性相关,矩阵
个行向量都线性相关,矩阵![]() 的任意
的任意![]() 级子式的行向量也线性相关. 由定理
级子式的行向量也线性相关. 由定理![]() ,这种子式全为零. 现在来证矩阵
,这种子式全为零. 现在来证矩阵![]() 中至少有一个
中至少有一个![]() 级子式不为零. 因为
级子式不为零. 因为
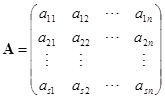
的秩为![]() ,所以在
,所以在![]() 中有
中有![]() 个行向量线性无关,譬如说,就是前
个行向量线性无关,譬如说,就是前![]() 个行向量. 把这
个行向量. 把这![]() 行取出来. 作一新的矩阵
行取出来. 作一新的矩阵
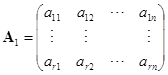 .
.
显然矩阵![]() 的行秩为
的行秩为![]() ,因此它的列秩也是
,因此它的列秩也是![]() ,这就是说,在
,这就是说,在![]() 中有
中有![]() 列线性无关. 不妨假设前
列线性无关. 不妨假设前![]() 列线性无关,因之,行列式
列线性无关,因之,行列式
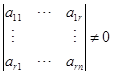 .
.
它就是矩阵![]() 中一个
中一个![]() 级子式. 这就证明了必要性.
级子式. 这就证明了必要性.
再证充分性. 设在![]() 中有一
中有一![]() 级子式不为零,而所有的
级子式不为零,而所有的![]() 级子式全为零. 我们证明
级子式全为零. 我们证明![]() 的秩为
的秩为![]() .
.
首先我们指出,由行列式按一行展开的公式可知,如果![]() 的
的![]() 级子式为零,那么
级子式为零,那么![]() 的
的![]() 级子式也一定为零,从而
级子式也一定为零,从而![]() 的所有级数大于
的所有级数大于![]() 的子式全为零.
的子式全为零.
设![]() 的秩为
的秩为![]() . 由必要性,
. 由必要性,![]() 不能小于
不能小于![]() ,否则
,否则![]() 的
的![]() 级子式就全为零了. 同样,
级子式就全为零了. 同样,![]() 也不能大于
也不能大于![]() ,否则
,否则![]() 就要有一个
就要有一个![]() 级子式不为零,而按照假定这是不可能的. 因之
级子式不为零,而按照假定这是不可能的. 因之![]() ,这就是我们要证明的结论.
,这就是我们要证明的结论.
从定理的证明可以看出,这个定理实际上包含两部分,一部分是,矩阵![]() 的秩
的秩![]() 的充分必要条件是为
的充分必要条件是为![]() 有一个
有一个![]() 级子式不为零;另一部分是,矩阵
级子式不为零;另一部分是,矩阵![]() 的秩
的秩![]() 的充分必要条件为
的充分必要条件为![]() 的所有
的所有![]() 级子式全为零. 有时候,这两个结论可以分开来用.从定理的证明还可以看出,在秩为
级子式全为零. 有时候,这两个结论可以分开来用.从定理的证明还可以看出,在秩为![]() 的矩阵中,不为零的
的矩阵中,不为零的![]() 级子式所在的行正是它行向量组的一个极大线性无关组,所在的列正是它列向量组的一个极大线性无关组.
级子式所在的行正是它行向量组的一个极大线性无关组,所在的列正是它列向量组的一个极大线性无关组.
最后我们来看一下,怎样计算一个矩阵的秩. 在前面,作为解线性方程组的一个方法,我们对矩阵作行的初等交换,把矩阵化成阶梯形. 实际上,这也是计算矩阵的秩的一个方法.
首先,矩阵的初等行变换是把行向量组变成一个与之等价的向量组. 我们知道,等价的向量组有相同的秩,因此,初等行变换不改变矩阵的秩. 同样地,初等列变换也不改变矩阵的秩.
其次,阶梯形矩阵的秩就等于其中非零的行的数目. 为了证明这个结论,只要证明在阶梯形矩阵中那些非零的行线性无关就行了. 设![]() 是一阶梯形矩阵,不为零的行数是
是一阶梯形矩阵,不为零的行数是![]() . 因为初等列变换部改变矩阵的秩,所以适当变换列的顺序,不妨设
. 因为初等列变换部改变矩阵的秩,所以适当变换列的顺序,不妨设
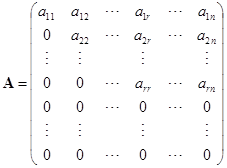 ,
,
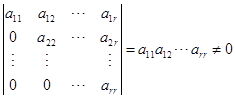 ,
,
因此,![]() 的秩为
的秩为![]() .
.
上面的讨论说明,为了计算一个矩阵的秩,只要用初等行变换把它变成阶梯形,这个阶梯形矩阵中非零的行的个数就是原来矩阵的秩.
以上的讨论还说明了,用初等变换化一个线性方程组成阶梯形,最后留下来的方程的个数与变换的过程无关,因为它就等于增广矩阵的秩.